Exercice : Calculatrice
Une entreprise vend des calculatrices d'une certaine marque.
Le service après-vente s'est aperçu qu'elles pouvaient présenter deux types de défaut,
l'un lié au clavier et l'autre lié à l'affichage.
Des études statistiques ont permis à l'entreprise d'utiliser la modélisation suivante :
La probabilité pour une calculatrice tirée au hasard de présenter un défaut de clavier est égale à 0,04.
En présence du défaut de clavier, la probabilité que la calculatrice soit en panne d'affichage est de 0,03.
Alors qu'en l'absence de défaut de clavier, la probabilité de ne pas présenter de défaut d'affichage est de 0,94.
On note :
C l'évènement : " la calculatrice présente un défaut de clavier ",
A l'évènement " la calculatrice présente un défaut d'affichage ".
Dans cet exercice, les probabilités seront écrites sous forme de nombres décimaux arrondis au millième.
Question
1. a. Préciser à l'aide de l'énoncé les probabilités suivantes :
\(P _{\overline{C}}(A),P_C(A) et P(C)\).
Solution
\(P _{\overline{C}}(A)=1-P _{\overline{C}}(\overline{A})=1-0,94=0,06\)
\(P_C(A)=0,03\)
\(P(C)=0,04\).
Question
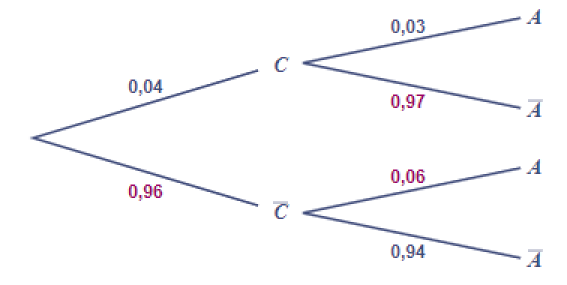
b. Construire un arbre pondéré décrivant cette situation.
Question
2. On choisit une calculatrice de cette marque au hasard.
a. Calculer la probabilité pour que la calculatrice présente les deux défauts.
Solution
\(p(C \cap A)= p(C) \times p_C(A)=0,04 \times 0,03=0,0012\) soit 0,12% de chance.
Ainsi, la probabilité pour que la calculatrice présente les deux défauts est 0,0012.
Question
b. Calculer la probabilité pour que la calculatrice présente le défaut d'affichage mais pas le défaut de clavier.
Solution
\(p(\overline{C})=1−p(C)=0,96\)
donc \(p(\overline{C}∩A)=p_{\overline{C}}(A)×p(\overline{C})=0,06 \times 0,96=\)0,0576
Ainsi, la probabilité pour que la calculatrice présente le défaut d'affichage mais pas le défaut de clavier est 0,0576.
Question
c. En déduire la probabilité pour que la calculatrice présente le défaut d'affichage.
Solution
D'après la formule des probabilités totales :
p(A)=p(C∩A)+p(C∩A)=0,0012+0,0576=0,0588
La probabilité que la calculatrice présente un défaut d'affichage est 0,0588.
Question
d. Montrer que la probabilité de l'événement D «la calculatrice est de fabrication défectueuse » est égale à 0,0976.
Solution
L'évènement D est l'événement « la calculatrice a un défaut de clavier ou un défaut d'affichage »
p(C∪A)=p(C)+p(A)−p(C∩A)=0,04+0,0588−0,0012=0,0976
D est l'évènement contraire de l'évènement « la calculatrice n'a aucun défaut » ,
\(p(D)=1−p(\overline{C}∩\overline{A})=1−p_{\overline{C}}(\overline{A})×p(\overline{C})=1−0,94×0,96=0,0976\)
La probabilité de l'évènement D «la calculatrice est de fabrication défectueuse » est égale à 0,0976.