Exercice : Centre Loisir
Un centre de loisirs destiné aux jeunes de 11 ans à 18 ans compte 60% de collégiens et 40% de lycéens.
Le directeur a effectué une étude statistique sur la possession de téléphones portables.
Cette étude a montré que 80% des jeunes possèdent un téléphone portable et que, parmi les collégiens,
70% en possèdent un.
On choisit au hasard un jeune du centre de loisirs et on s'intéresse aux événements suivants :
C : "le jeune choisi est un collégien" ;
L : "le jeune choisi est un lycéen" ;
T : "le jeune choisi possède un téléphone portable"
Question
1. Donner les probabilités : \(p(C),p(L),p(T),p_C(T).\)
Solution
\(p(C) =\frac{60}{100}=0,6\)
\(p(L) =\frac{40}{100}= 0,4\)
\(p(T) =\frac{80}{100}= 0,8\)
\(p_C(T) =\frac{70}{100}\)
Question
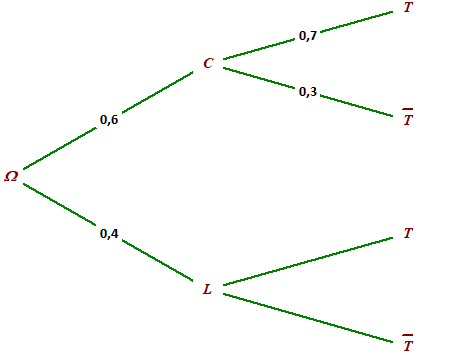
2.Faire un arbre de probabilités représentant la situation et commencer à la renseigner avec les données de l'énoncé.
Question
3. Calculer la probabilité que le jeune choisi soit un collégien possédant un téléphone portable.
Solution
D'après la définition des probabilités conditionnelles, on a :
\(p_C(T) =\frac{p(C \cap T)}{p(C)}\)
\(0,7 =\frac{p(C \cap T)}{0,6}\)
\(p(C \cap T ) = 0, 7 \times 0,6\)
\(p(C \cap T) = 0,42\)
Question
4.Calculer la probabilité que le jeune choisi soit un collégien sachant qu'il possède un téléphone portable.
Solution
\(p_T(C)=\frac{p(T \cap C)}{p(T)}\)
\(p_T(C)=\frac{0,42}{0,8}\)
\(p_T(C)= 0,525\)
Question
5.a. Calculer \(p(T \cap L)\), en déduire \(p_L(T)\).
Solution
Les deux événements C et L forment une partition de l'univers :
\(C \cap L= ∅\) : un jeune ne peut être un collégien et un lycéen en même temps;
\(C \cup L= Ω\)
donc p(C)+p(L)=0,6+0,4=1
D'après la formule des probabilités totales, on a :
\(p(T) =p(C \cap T) + p(L \cap T)\)
\(0,8 = 0,42 + p(L \cap T)\)
donc \(p(L \cap T) = 0,8-042=0,38\)
D'après la définition des probabilités conditionnelles, on a :
\(p_L(T) =\frac{p(L \cap T)}{p(L)}\)
\(p_L(T) =\frac{0,38}{0,4}\)
\(p_L(T) = 0,95\)
Question
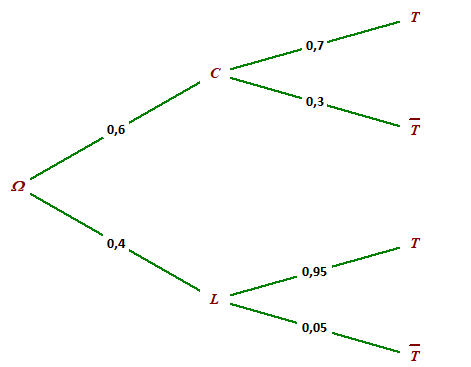
b.Compléter l'arbre construit dans la question 2.