Exercice : Champignon
Un stock de champignons est constitué de trois variétés de champignons conditionnés en barquettes.
Ces barquettes proviennent exclusivement de France ou d'Italie.
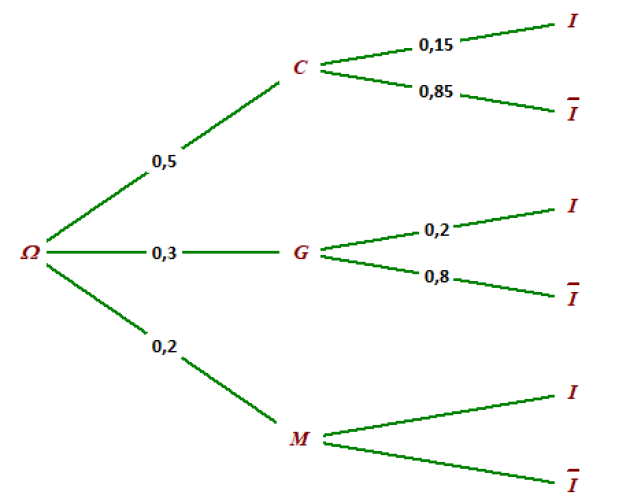
Ce stock est composé de 50% de barquettes de cêpes, 30% de barquettes de girolles et de 20% de barquettes de morilles.
15 % des barquettes de cêpes proviennent d'Italie.
20 % des barquettes de girolles proviennent d'Italie.
21,5 % des barquettes proviennent d'Italie.
On choisit une barquette de ce stock au hasard.
On notera les événements suivants :
– C : « La barquette choisie contient des cêpes » ;
– G : « La barquette choisie contient des girolles » ;
– M : « La barquette choisie contient des morilles » ;
– I : « La barquette choisie provient d'Italie » ;
– F : « La barquette choisie provient de France ».
Question
1. Quelle est la probabilité que la barquette choisie contienne des cêpes et provienne d'Italie ?
Solution
\(p(C \cap I)=0,5 \times 0,15=0,075\)
Question
2. Quelle est la probabilité que la barquette choisie contienne des cèpes et provienne de France ?
Solution
\(p(C \cap \overline{I})=0,5 \times 0,85=0,425\)
Question
3. Montrer que la probabilité que la barquette de morille provienne d'Italie est 0,4.
Solution
\(p(I)=p(I \cap C)+p(I \cap G)+p(I \cap M)=0,075+0,3 \times 0,2+p(I \cap M)= 0,215\). d'après la formules des probabilités totales.
\(0,075+0,06+p(I \cap M)= 0,215.\)
\(0,135+p(I \cap M)= 0,215.\)
\(p(I \cap M)=0,215-0,135=0,08\)
or \(p_M(I)=\frac{p(I \cap M)}{p(M})\)
donc \(p_M(I)=\frac{p(I \cap M)}{p(M})=\frac{0,08}{0,2}=0,4\)
donc 40% des morilles proviennent d'Italie.
Question
4. Quelle est la probabilité que la barquette choisie contienne des cèpes sachant que cette barquette provient d'Italie ? On donnera une valeur arrondie à \(10^{−3}\) .
Solution
La probabilité que la barquette choisie contienne des cèpes sachant que cette barquette provient d'Italie est \(p_I(M)=\frac{p(I \cap M)}{p(I)}=\frac{0,08}{0,215}\simeq0,372\) soit environ 37,2% de chance.
Question
5. La barquette choisie provient de France. Quelle est la probabilité que ce soit une barquette de girolles ? On donnera une valeur arrondie à \(10^{−3 }\).
Solution
\(p_F(G)=\frac{p(F \cap G)}{p(\overline{I})}=\frac{0,8 \times 0,3}{1-0,215}=\frac{0,24}{1-0,215}\simeq0,306\) soit environ 30,6% de chance.