Exercice : Chattons
Madame Boulard fait un très grand élevage de chats de races.
Elle possède des Siamois, des Birmans et des Abyssins.
Le printemps dernier, pratiquement toutes ses femelles ont eu des bébés et Madame Boulard a mis une annonce pour signaler qu'elle avait une très grande quantité de petits chatons à vendre.
On sait que :
32% des chatons sont des Siamois, 54% des chatons sont des Abyssins et le reste est constitué de Birmans.
Parmi les Siamois, 54 % sont des mâles
66 % des Abyssins sont des femelles.
l y a au total 40,96 % de chatons mâles.
Un petit garçon, Pierre, vient acheter un chaton avec sa mère.
Comme ils sont tous adorables et qu' il n'arrive pas à choisir, Pierre décide de le prendre au hasard.
On désigne par S, B, A, M et F les événements suivants :
S : " Pierre achète un chaton Siamois ".
B : " Pierre achète un chaton Birman ".
A : " Pierre achète un chaton Abyssin ".
M : " Pierre achète un chaton mâle ".
F : " Pierre achète un chaton femelle "
Question
1. a. Traduire les données de l'énoncé en langage de probabilités.
Solution
p(S)=0,32 p(A)=0,54 et p(B)=1−(0,32+0,54)=0,14
\(p_S(M)=0,54\)
\(p_A(F)=0,66\)
\(p(M)=0,4096\)
Question
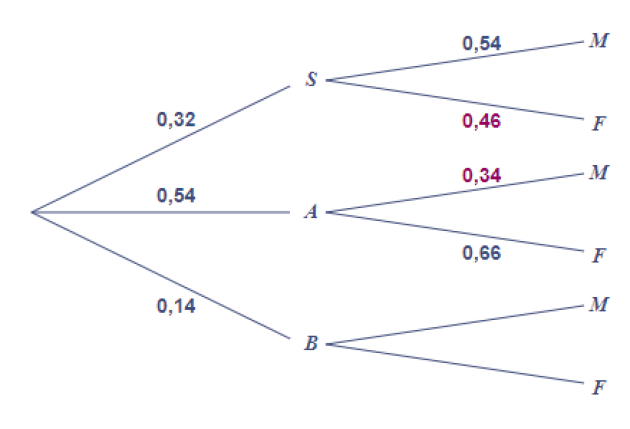
b. Construire un arbre illustrant la situation, en indiquant sur chaque branche les probabilités données
dans l'énoncé, les probabilités manquantes seront calculées dans les questions ultérieures.
Question
2.a. Déterminer la probabilité que Pierre achète un chaton mâle Siamois.
Solution
a.p(M∩S)=\(p_S\)(M)×p(S)=0,54×0,32=0,1728
La probabilité que Pierre achète un chaton mâle Siamois est égale à 0,1728.
Question
b. Calculer \(p(M \cap A)\) et interpréter ce résultat à l'aide d'une phrase.
Solution
\(p(M∩A)=p_A(M)×p(A)\)
\(p_A(M)=1−p_A(F)=1−0,66=0,34\)
p(M∩A)=0,34×0,54=0,1836
La probabilité que Pierre achète un chaton mâle Abyssin est égale à 0,1836.
Question
c. En déduire que la probabilité que Pierre achète un chaton mâle Birman est égale à 0,0532:
Solution
S, A et B forment une partition de l'univers alors, d'après la formule des probabilités totales :
p(M)=p(M∩S)+p(M∩A)+p(M∩B)
Donc p(M∩B)=p(M)−p(M∩S)−p(M∩A)=0,4096−0,1728−0,1836=0,0532
La probabilité que Pierre achète un chaton mâle Birman est égale à 0,0532.
Question
d. Le chaton acheté par Pierre est un, Birman. Quelle est la probabilité que ce soit un mâle ?
Solution
\(p_B(M)=\frac{p(M∩B)}{p(B)}=\frac{0,0532}{0,14}\)=0,38
La probabilité que le chaton acheté soit un mâle, sachant que c'est un Birman est égale à 0,38.