Exercice : Autoroute
A une sortie d'autoroute, la gare de péage comporte trois voies.
Une étude statistique a montré que :
28% des automobilistes empruntent la voie de gauche, réservée aux abonnées;
un automobiliste empruntant cette voie franchit toujours le péage en moins de 10 secondes;
52% des automobilistes empruntent la voie du centre,réservée au paiement par carte bancaire;
parmi ces derniers, 75% franchissent le péage en moins de 10 secondes;
les autres automobilistes empruntent la voie de droite en utilisant un autre moyen de paiement (pièces ou billets)
On choisit un automobiliste au hasard et on considère les événements suivants :
G : "l'automobiliste emprunte la voie de gauche" ;
C : "l'automobiliste emprunte la voie du centre" ;
D : "l'automobiliste emprunte la voie de droite" ;
T : "l'automobiliste franchit le péage en moins de 10 secondes"
Question
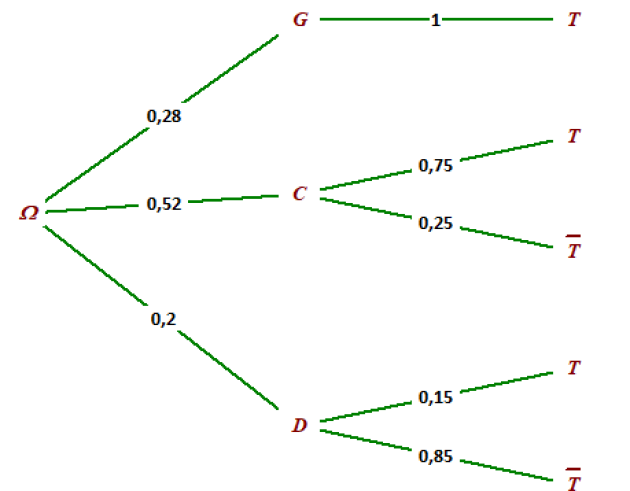
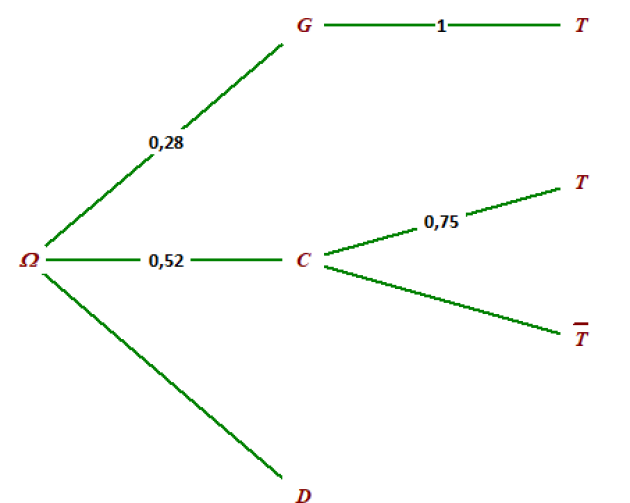
1. Construire un arbre pondéré traduisant cette situation.
Cet arbre sera complété au fur et à mesure de l'exercice.
Question
2. Calculer la probabilité \(p(C \cap T)\)
Solution
D'après la définition des probabilités conditionnelles, on a :
\(p_C(T) =\frac{p(C \cap T)}{p(C)}\)
\(\iff 0,75 =\frac{p(C \cap T)}{0,52}\)
\(\iff p(C \cap T) = 0,75 \times 0,52\)
\(\iff p(C \cap T) = 0,39\)
3. L'étude a aussi montré que 70% des automobilistes passent le péage en moins de 10 secondes.
Question
a. Justifier que \(p(D \cap T)=0,03\)
Solution
L'information supplémentaire donnée dans l'énoncé permet d'écrire :
p(T) = 0,7
Les événements G, C et D forment une partition de l'univers :
\(G \cup C \cup D=Ω\) : la gare de péage comporte trois voies.
Les évéments G, C et D sont disjoints deux à deux :
un automobilistes ne peut pas prendre deux voies à la fois.
D'après la formule des probabilités totales, on a :
\(p(T) = p(G \cap T) + p(C \cap T) + p(D\cap T)\)
\(\iff 0,7 = 0,28 + 0,39 + p(D \cap T)\)
\(\iff 0,7 = 0;67 + p(D \cap T)\)
\(\iff p(D \cap T) = 0;7 - 0,67\)
\(\iff p(D \cap T) = 0,03\)
Question
b.Calculer la probabilité qu'un automobiliste empruntant la voie de droite passe le péage en moins de 10 secondes.
Solution
D'après la définition des probabilités conditionnelles, on a :
\(p_D(T) =\frac{p(D \cap T)}{p(D)}\)
\(\iff p_D(T) \frac{0,03}{1 - 0,28 - 0,52}\)
\(\iff p_D(T) =\frac{0,03}{0,2}\)
\(\iff p_D(T) = 0,15\)