Etude courbe
Question
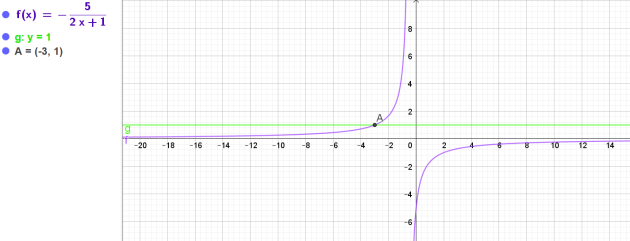
1) Représenter à l'aide de Geogebra la courbe de la fonction \(f\) définie par
\(f(x)=\frac{-5}{2x+1}\)
puis résoudre graphiquement l'inéquation \(f(x)\ge 1\).
Solution
\(\frac{-5}{2x+1}=1\)
-5=1\times (2x+1)
\(\Longleftrightarrow -5=2x+1\)
\(\Longleftrightarrow -5-1=2x\)
\(\Longleftrightarrow -6=2x\)
\(\Longleftrightarrow x=-3\)
\(f(x)=\frac{-5}{2x+1}\ge 1 \quad pour \quad x \in]-3;0[\)
Question
2) Montrer que pour tout \(x\) réel :
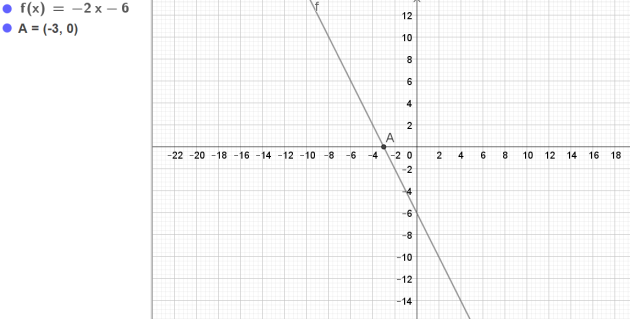
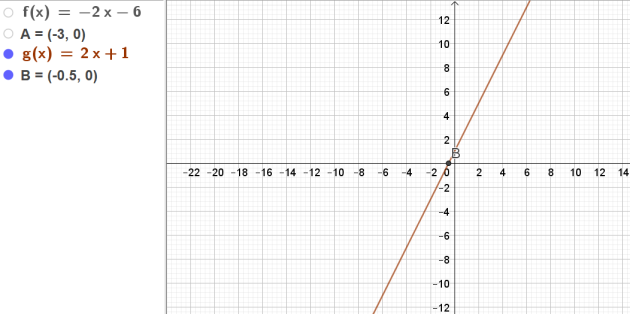
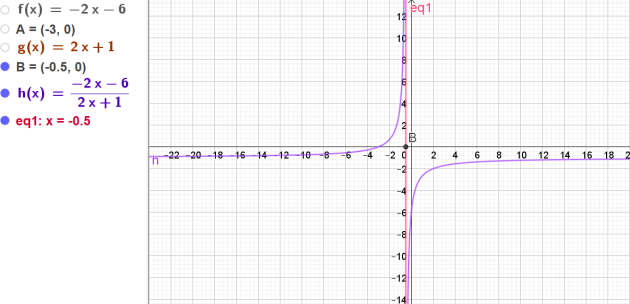
\(\frac{-5}{2x+1}-1=\frac{-2x-6}{2x+1}\) puis résoudre l'inéquation
\(f (x) -1\ge 0\) à l'aide d'un tableau de signes. Comparer avec la réponse du 1.
Solution
\(\frac{-5}{2x+1}-1\)
\(=\frac{-5}{2x+1}-\frac{2x+1}{2x+1}\)
\(=\frac{-5-2x-1}{2x+1}\)
\(=\frac{-6-2x}{2x+1}\)
\(=\frac{-2x-6}{2x+1}\)
\(-2x-6=0 \Longleftrightarrow -2x=6 \Longleftrightarrow x=-3\)
\(2x+1=0 \Longleftrightarrow 2x=-1 \Longleftrightarrow x=-\frac{1}{2}\)
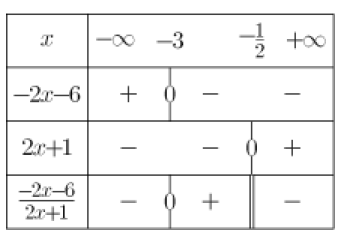
\(\frac{-5}{2x+1}-1 \ge 0 \Longleftrightarrow \frac{-2x-6}{2x+1}\ge 0 \Longleftrightarrow x \in [-3;-\frac{1}{2}[\)