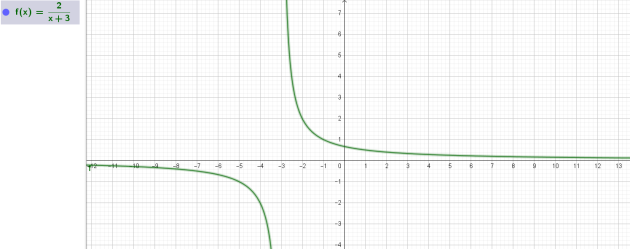
Décroissante
On appelle f la fonction définie sur
\(I=\mathbb{R}\)\{-3} par \(f(x) = \frac{2}{x+3}\).
Question
1.Démontrer que -3 est effectivement la valeur interdite de la fonction \(f\)
Solution
\(x+3=0 \Longleftrightarrow x=-3\)
Question
2. a Prouver que pour tous réels a et b de I : \(f(b) -f(a) = \frac{2(a-b)}{(a+3)(b+3)}\)
Solution
\(f(a) = \frac{2}{a+3}\)
\(f(b) = \frac{2}{b+3}\)
\(f(b) -f(a)= \frac{2}{b+3}-\frac{2}{a+3}\)
\(f(b) -f(a)= \frac{2(a+3)}{(b+3)(a+3)}-\frac{2(b+3)}{(b+3)(a+3)}\)
\(f(b) -f(a)= \frac{2(a+3)-2(b+3)}{(b+3)(a+3)}\)
\(f(b) -f(a)= \frac{2a+6-2b-6)}{(b+3)(a+3)}\)
\(f(b) -f(a)= \frac{2a-2b}{(b+3)(a+3)}\)
\(f(b) -f(a)= \frac{2(a-b)}{(a+3)(b+3)}\)
Question
b. En déduire les variations de \(f\) sur \(] -3;+\infty[\) puis sur \(] -\infty;-3[\)
Indice
On doit séparer les deux intervalles car -3 est la valeur interdite de la fonction \(f\)
Solution
On doit séparer les deux intervalles car -3 est la valeur interdite de la fonction \(f\)
A. \(\color{magenta}{Sur \quad ] -3;+\infty[}\)
a+3>0
b+3>0
donc (a+3)(b+3)>0
Si b>a alors a-b<0
donc si b>a \(\frac{2(a-b)}{(a+3)(b+3)}<0\)
donc si b>a \(f(b)-f(a)<0\)
donc si b>a \(f(b)<f(a)\)
La fonction f est donc décroissante sur l'intervalle \(] -3;+\infty[.\)
B. \(\color{magenta}{Sur \quad ] -\infty;-3[}\)
a+3<0
b+3<0
donc (a+3)(b+3)>0 car
\(\color{red}{\textbf{Le produit de deux nombres négatifs donne un résultat positif.}}\)\(( "-"\times "-"\rightarrow "+")\)
Si b>a alors a-b<0
donc si b>a \(\frac{2(a-b)}{(a+3)(b+3)}<0\)
donc si b>a \(f(b)-f(a)<0\)
donc si b>a \(f(b)<f(a)\)
\(La fonction f est donc décroissante sur l'intervalle ] -\infty;-3[\).