Eleve comparaison
Question
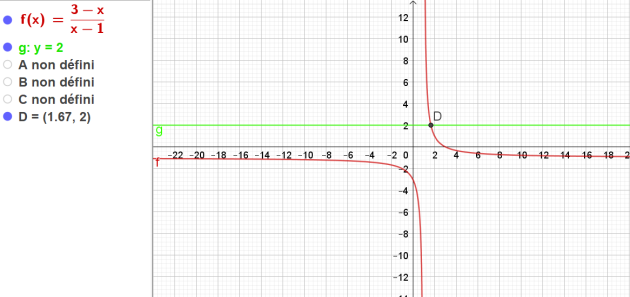
Un élève dit que le quotient
\(\frac{3-x}{x-1}\) donne un résultat inférieur ou égal à 2 quel que
soit le nombre \(x\) choisi, a-t-il raison ?
Solution
Résolvons l'équation \(\frac{3-x}{x-1}\le 2\):
\(\frac{3-x}{x-1}-2 \le 0\)
\(\frac{3-x}{x-1}-2\frac{x-1}{x-1} \le 0\)
\(\frac{3-x-2(x-1)}{x-1} \le 0\)
\(\frac{3-x-2x+2}{x-1} \le 0\)
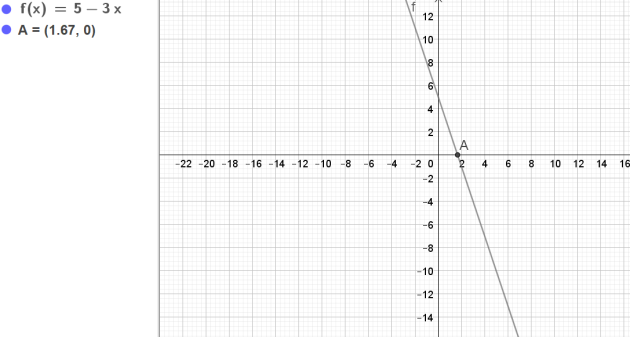
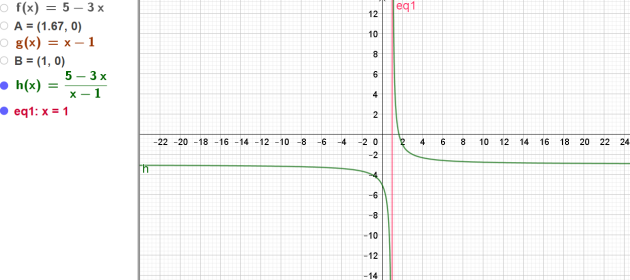
\(\frac{5-3x}{x-1} \le 0\)
\(5-3x=0 \Longleftrightarrow -3x=-5\Longleftrightarrow x=\frac{5}{3}\)
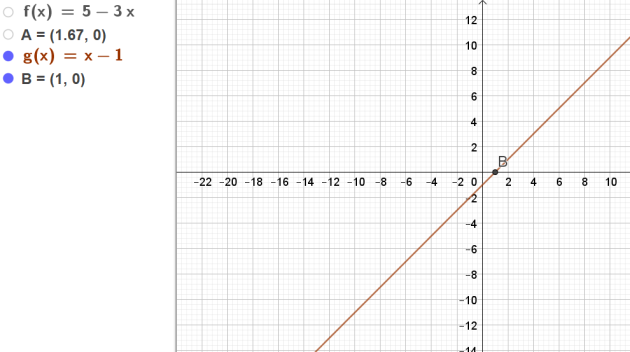
\(x-1=0 \Longleftrightarrow x=1\)
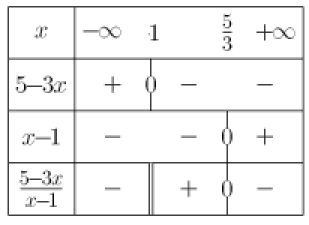
\(\frac{3-x}{x-1}\le 2\)
\(\Longleftrightarrow \frac{3-x}{x-1}-2 \le 0\)
\(\Longleftrightarrow \frac{5-3x}{x-1} \le 0\)
\(\Longleftrightarrow x\in ]-\infty;1[\cup[\frac{5}{3};+\infty[\)