Fonction inverse
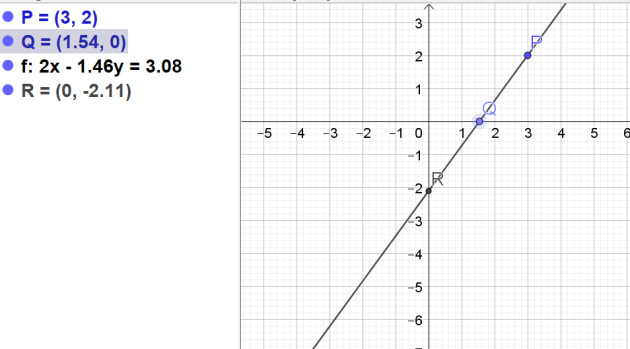
Dans un repère orthonormé, on considère le point P (3;2).
Soit Q un point quelconque de l'axe des abscisses.
Soit R l'intersection de la droite (PQ) avec l'axe des ordonnées.
On note X l'abscisse de Q et Y l'ordonnée de R.
Question
1.Exprimer en fonction de X (abscisse du point Q) le coefficient directeur de la droite (PQ)
Solution
\(a=\frac{y_Q-y_P}{x_Q-x_P}=\frac{0-3}{X-2}=\frac{-3}{X-2}\)
Question
2. Trouver en fonction de X l'équation de la droite (PQ).
Solution
\(y=ax+b=\frac{-3}{X-2}x+b\)
or la droite passe par le point P donc
\(2=\frac{-3}{X-2} \times 3+b\)
\(2=\frac{-9}{X-2}+b\)
\(b=2-\frac{-9}{X-2}\)
\(b=2+\frac{9}{X-2}\)
donc l'équation de la droite (PQ) est :
\(y=\frac{-3}{X-2}x+2+\frac{9}{X-2}\)
Question
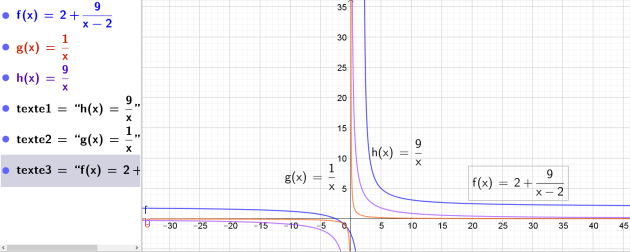
Etudier la fonction f∶ X → Y
Solution
Pour le point R : \(x=0\)
or ce point est situé sur la droite (PQ ) donc \(Y=2+\frac{9}{X-2}\)
La courbe de la fonction \(\frac{9}{x}\) se déduit de celle de la fonction \(\frac{1}{x}\) par une affinité de rapport 9.
L'ordonnée Y du point R décrit donc une hyperbole qui se déduit de la courbe de la fonction \(\frac{9}{x}\):
par une translation verticale de 2 unité vers le haut
une translation horizontale de 2 unités vers la droite.