Résolution Inequations
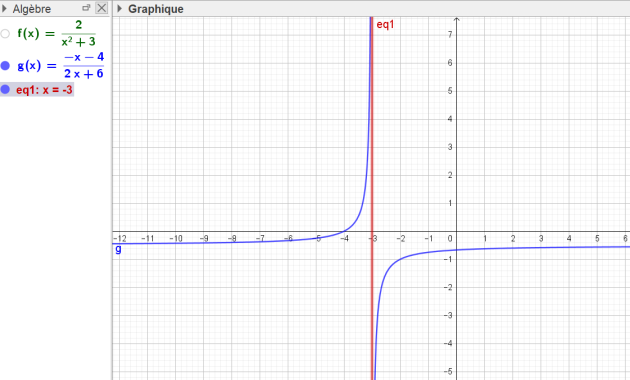
On a représenté ci-contre la courbe représentative de la fonction f définie par
\(f(x)=\frac{-x-4}{2x+6}\)
Question
1) Donner la valeur interdite. Faire apparaître cette valeur sur l'axe des abscisses.
Solution
\(2x+6=0 \Longleftrightarrow 2x=-6\)\(\Longleftrightarrow x=-3\)
La valeur interdite est donc \(x=-3\)
Question
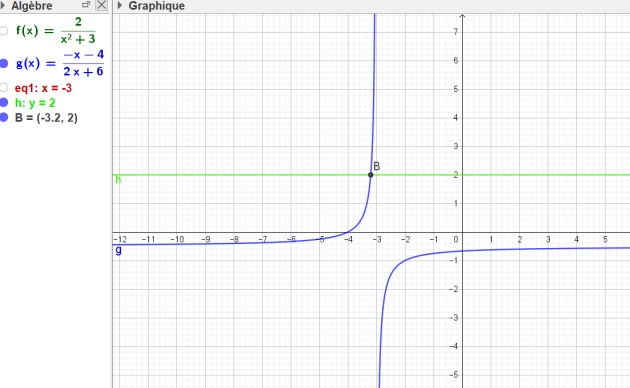
2) Résoudre par le calcul l'équation \(f(x)=2\) puis contrôler graphiquement.
Solution
\(\frac{-x-4}{2x+6}=2\)
\(-x-4=2\times (2x+6)\)
\(-x-4=4x+12\)
\(-x=4x+12+4\)
\(-x-4x=12+4\)
\(-5x=16\)
\(x=\frac{16}{-5}=-3,2\)
\(\color{red}{x=-3,2}\)
Question
3) Résoudre graphiquement les inéquations
a. \(f(x)>2\)
Solution
\(x \in ]-3,2;-3[\)
Question
b) \(f (x)\ge 3\)
Indice
a. Résoudre l'équation \(\frac{-x-4}{2x+6}= 3\)
b. Résoudre graphiquement l'inéquation \(\frac{-x-4}{2x+6}\ge 3\)