Croissante
Question
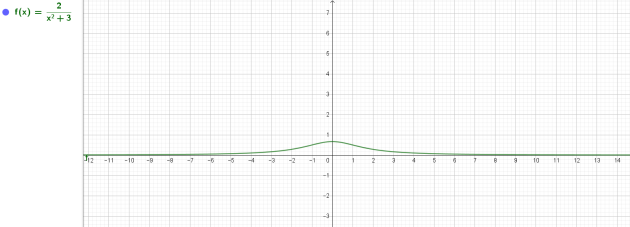
g est la fonction définie sur \(\mathbf{R}\) par \(g(x) = \frac{2}{x^2+3}\).
Question
1.Démontrer que la fonction g n'admet pas de valeur interdite
Solution
\(x^2+3=0\) ne s'annule jamais car un carré est toujours positif
donc \(x^2>0 \Longleftrightarrow x^2+3>0\)
Question
2.a. Prouver que pour tous réels a et b \( g(b) - g(a) = \frac{2(a^2-b^2)}{(a^2+3)(b^2+3)}\).
Solution
\(g(a) = \frac{2}{a^2+3}\)
\(g(b) = \frac{2}{b^2+3}\)
\(g(b) - g(a) = \frac{2}{b^2+3}-\frac{2}{a^2+3}\)
\(g(b) - g(a) = \frac{2(a^2+3)}{b^2+3}-\frac{2(b^2+3)}{a^2+3}\)
\(g(b) - g(a) = \frac{2(a^2+3)}{(a^2+3)((b^2+3)}\)\(-\frac{2(b^2+3)}{(a^2+3)(b^2+3)}\)
\(g(b) - g(a) = \frac{2(a^2+3)-2(b^2+3)}{(a^2+3)(b^2+3)}\)
\(g(b) - g(a) = \frac{2a^2+6-2b^2-6}{(a^2+3)(b^2+3)}\)
\(g(b) - g(a) = \frac{2a^2-2b^2}{(a^2+3)(b^2+3)}\)
\(g(b) - g(a) = \frac{2(a^2-b^2)}{(a^2+3)(b^2+3)}\)
Question
b. Etablir que g est strictement croissante sur \(\mathbb{R}^-\)\(=]-\infty;0]\)et strictement décroissante sur \(\mathbb{R}^+\)\(=[0 ;+\infty[\)
Solution
\(g(b) - g(a) = \frac{2(a^2-b^2)}{(a^2+3)(b^2+3)}\)
\(g(b) - g(a) = \frac{2(a+b)(a-b)}{(a^2+3)(b^2+3)}\)
en effet \(\color{red}{a^2-b^2=(a+b)(a-b)}\) (identité remarquable)
\(\color{magenta}{Sur \quad \mathbf{R}}\)
\(a^2+3>0\)
\(b^2+3>0\)
donc \((a^2+3)(b^2+3)>0\)
Si b>a alors a-b<0
A. \(\color{magenta}{Sur \quad \mathbb{R}^+}\)
a>0
b>0
donc a+b>0
(a+b)(a-b)<0
\(\color{red}{\textbf{Le produit d'un nombre négatif et d'un nombre positif donne un résultat négatif. }"-" \times "+" \rightarrow "-"}\)
donc \(\frac{2(a+b)(a-b)}{(a^2+3)(b^2+3)}<0\)
donc si b>a \(f(b)-f(a)<0\)
donc si b>a \(f(b)<f(a)\)
\(\color{red}{\textbf{La fonction f est donc strictement décroissante sur }\mathbb{R}^+}\).
B. \(\color{magenta}{Sur \quad \mathbb{R}^-}\)
a<0
b<0
donc a+b<0
(a+b)(a-b)>0
\(\color{red}{\textbf{Le produit de deux nombres négatifs donne un résultat positif. }"-" \times "-" \rightarrow "+"}\)
donc \(\frac{2(a+b)(a-b)}{(a^2+3)(b^2+3)}>0\)
donc si b>a \(f(b)-f(a)>0\)
donc si b>a \(f(b)>f(a)\)
\(\color{red}{\textbf{La fonction f est donc strictement croissante sur }\mathbb{R}^-}\).