Exercice : Jeu arrêté
Deux joueurs A et B jouent avec une pièce de monnaie équilibrée. Ils se mettent d'accord sur les règles suivantes :
A parie sur l'apparition de trois fois Pile
B sur l'apparition de trois fois Face.
Ils misent la même somme : 32 € chacun, dans le pot commun.
Celui qui gagne emporte l'ensemble du pot.
Au premier lancer, Pile sort. Aussitôt après, le jeu doit s'arrêter pour une raison inconnue.
B veut que la partie soit annulée et les mises rendues à chaque joueur, mais A n'est pas d'accord, il veut que l'on répartisse équitablement le pot commun en sachant que Pile était déjà sorti une fois.
Question
Combien faudrait-il donner à chacun selon A ?
Solution
Arbre de probabilité à partir du deuxième lancer :
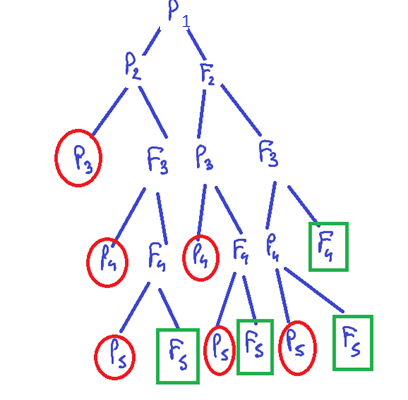
p("le joueur A gagne")=\((\frac{1}{2})^2+(\frac{1}{2})^3+(\frac{1}{2})^4+(\frac{1}{2})^3+(\frac{1}{2})^4+(\frac{1}{2})^4\)
p("le joueur A gagne")=\(\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+\frac{1}{8}+\frac{1}{16}+\frac{1}{16}\)
p("le joueur A gagne")=\(\frac{4}{16}+\frac{2}{16}+\frac{1}{16}+\frac{2}{16}+\frac{1}{16}+\frac{1}{16}=\color{red}{\frac{11}{16}}\)
p("le joueur B gagne")=\((\frac{1}{2})^4+(\frac{1}{2})^4+(\frac{1}{2})^4+(\frac{1}{2})^3=\frac{1}{16}+\frac{1}{16}+\frac{1}{16}+\frac{1}{8}\)
p("le joueur B gagne")=\(\frac{3}{16}+\frac{2}{16}=\color{red}{\frac{5}{16}}\)
ou p("le joueur B gagne")=1-p("le joueur A gagne") car les deux événements sont des événements contraires.
donc p("le joueur B gagne")= \(=1-\frac{11}{16}\)
Il faudrait donner \(\frac{11}{16} \times 64=\color{red}{44€}\) au joueur A
Il faudrait donner \(\frac{5}{16} \times 64=\color{red}{20€}\) au joueur B.