Exercice : Feux Rouges
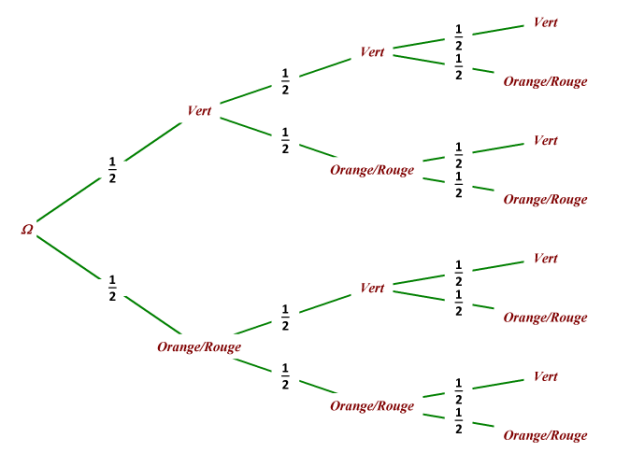
Pour se rendre à son travail, un automobiliste rencontre trois feux tricolores.
On suppose que les feux fonctionnent de manière indépendante, que l'automobiliste s'arrête s'il voit le feu orange ou rouge et qu'il passe si le feu est vert.
On suppose de plus que chaque feu est vert durant un temps égal à celui des feux rouge et orange réunis.
Autrement dit, l'automobiliste a autant de chance de passer que de s'arrêter.
Question
1.Compléter le tableau de la loi de la variable aléatoire comptant le nombre de feux verts rencontrés :
\(x_i\) | 0 | 1 | 2 | 3 |
|---|---|---|---|---|
\(p(X=x_i)\) |
Solution
\(x_i\) | 0 | 1 | 2 | 3 |
|---|---|---|---|---|
\(p(X=x_i)\) | \(\frac{1}{8}\) | \(\frac{3}{8}\) | \(\frac{3}{8}\) | \(\frac{1}{8}\) |
Question
2.Calculer l'espérance de cette variable. Que représente-t-elle ?
Solution
\(E(X)=\frac{1}{8}\times 0+\frac{3}{8} \times 1+\frac{3}{8}\times 2+\frac{1}{8} \times 3\)
\(E(X)=\frac{3}{8} +\frac{6}{8}+\frac{3}{8}\)
\(E(X)=\frac{12}{8}=1,5\)
\(\color{red}{\textbf{En moyenne en faisant un grand nombre de trajets, l'automobiliste rencontrera 1,5 feux verts sur son trajet.}}\)
Question
3.Calculer la variance et l'écart type de cette variable.
Solution
\(V(X)=\frac{1}{8}\times (0-1,5)^2+\frac{3}{8} \times (1-1,5)^2+\frac{3}{8}\times (2-1,5)^2+\frac{1}{8} \times (3-1,5)^2\)
\(V(X)=\frac{1}{8} \times 2,25+\frac{3}{8} \times 0,25 +\frac{3}{8}\times 0,25+\frac{1}{8} \times 2,25\)
\(V(X)=\frac{3}{4}=0,75\)
\(\sigma(X)=\sqrt{V(X)}\simeq0,87\)
\([E(X)-\sigma(X) ;E(X)+\sigma(X)]\simeq[1,5-0,87 ;1,5+0,87 ]\simeq[0,63 ;2,37 ]\mapsto \color{red}{\textbf{L'automobiiste a de fortes chances de rencontrer 1à 2 feux verts sur son parcours.}}\)
Question
4.Quelles informations peut-on en tirer ?
Solution
\(\color{red}{\textbf{On peut en déduire que sur un grand nombre de trajets, l'automobiliste rencontrera 1,5 feux verts sur les 3 feux.}}\)
\(\color{red}{\textbf{Mais avec de forte chance, il rencontre entre 1 et 2 feux verts sur son chemin.}}\)