Exercice : Roulette
La roulette est un jeu de hasard pour lequel chaque joueur peut miser au choix sur un numéro ou une famille de numéros.
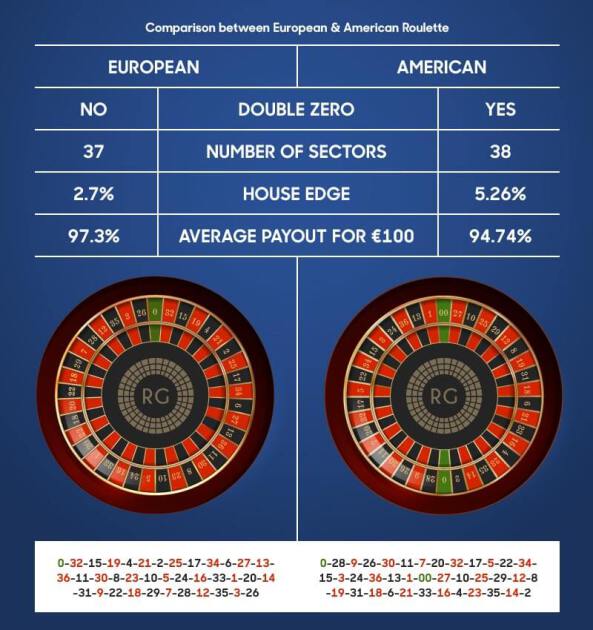
On considère une roulette européenne.
Le tirage au sort s'effectue avec une bille jetée dans une roue qui tourne. La bille s'arrête dans une encoche face à un numéro.
Le tableau ci-dessous résume les gains obtenus en fonction du pari effectué.
Dans le cas d'un succès, on récupère la mise et on obtient les gains suivants :
Type de pari | Gain |
|---|---|
Un seul numéro | 35 fois sa mise |
Tous les numéros de 1 à 12 | 2 fois sa mise |
Tous les numéros de 13 à 24 | 2 fois sa mise |
Tous les numéros de 25 à 36 | 2 fois sa mise |
Tous les numéros rouges | 1 fois sa mise |
Tous les numéros noirs | 1 fois sa mise |
Question
\(\color{magenta}{\textbf{Partie A :}}\)
On note X la variable aléatoire donnant le gain pour une mise de 1 euro dans le cas où le joueur parie sur le numéro 13.
a. Écrire la loi de probabilité de la variable aléatoire X.
b. Calculer l'espérance de la variable aléatoire X.
c. Dans le jargon du casino, l'espérance de la variable aléatoire X s'appelle l'"avantage de la maison". Expliquer cette expression.
d.Calculer la variance et l'écart type de la variable aléatoire X
Solution
\(x_i\) | -1 | 35 |
|---|---|---|
\(p(X=x_i)\) | \(\frac{36}{37}\) | \(\frac{1}{37}\) |
E(X)=\(\frac{36}{37}\times (-1)+\frac{1}{37}\times 35=\frac{-36+35}{37}=\frac{-1}{37}\simeq-0,027\)
\(\color{red}{\textbf{L'espérance étant négative, il s'agit donc de la somme perçue par le joueur et gagnée par le casino d'où le nom d'"avantage de la maison".}}\)
V(X)=\(\frac{36}{37}\times (-1-(\frac{-1}{37}))^2+\frac{1}{37}\times (35-\frac{-1}{37})^2\)
\(V(X)=\frac{36}{37}\times (-1+\frac{1}{37}))^2+\frac{1}{37}\times (35+\frac{1}{37})^2\)
V(X)\(=\frac{36}{37}\times (\frac{-37}{37}+\frac{1}{37}))^2+\frac{1}{37}\times (\frac{1295}{37}+\frac{1}{37})^2\)
V(X)\(=\frac{36}{37}\times (\frac{-36}{37})^2+\frac{1}{37}\times (\frac{1296}{37})^2\)
V(X)\(=\frac{36}{37} \times \frac{1296}{1369}+\frac{1}{37}\times \frac{1 679 616}{1369}\)
V(X)\(=\frac{36 \times 1296}{50653}+\frac{1 \times 1 679 616}{50653}\)
V(X)\(=\frac{46 656 +1 679 616}{50653}\)
V(X)\(=\frac{1 726 272}{50653}\simeq34,1\)
\(\sigma(X)=\sqrt{34,1}\simeq5,84\)
\([E(X)-\sigma(X) ;E(X)+\sigma(X)]\simeq[-0,027-5,84 ; -0,027+5,84]\simeq[-5 ,87; 5,82]\)
\(\color{red}{\textbf{Le "gain" du joueur a de fortes chances de se trouver entre -5,87€ et 5,82€}}\)
Question
\(\color{magenta}{\textbf{Partie B :}}\)
On note Y la variable aléatoire donnant le gain pour une mise de 1 € dans le cas où un joueur parie sur les numéros 25 à 36.
a. Écrire la loi de probabilité de la variable aléatoire Y.
b. Calculer l'espérance de la variable aléatoire Y.
c. Calculer la variance et l'écart type de la variable aléatoire Y.
Solution
\(y_i\) | -1 | 2 |
|---|---|---|
\(p(Y=y_i)\) | \(\frac{25}{37}\) | \(\frac{12}{37}\) |
E(Y)=\(\frac{25}{37}\times (-1)+\frac{12}{37}\times 2=\frac{-25+24}{37}=\frac{-1}{37}\simeq-0,027\)
\(\color{red}{\textbf{Le joueur perd donc en moyenne sur un grand nombre de parties } \frac{1}{37} \textbf{ de sa mise.Il s'agit de la même somme que dans le cas précédent.}}\)
V(Y)=\(\frac{25}{37}\times (-1-(\frac{-1}{37}))^2+\frac{12}{37}\times (2-\frac{-1}{37})^2=\frac{25}{37}\times (-1+\frac{1}{37}))^2+\frac{12}{37}\times (2+\frac{1}{37})^2\)
V(Y)\(=\frac{25}{37}\times (\frac{-37}{37}+\frac{1}{37}))^2+\frac{12}{37}\times (\frac{74}{37}+\frac{1}{37})^2\)
V(Y)\(=\frac{25}{37}\times (\frac{-36}{37})^2+\frac{12}{37}\times (\frac{75}{37})^2\)
V(Y)\(=\frac{25}{37} \times \frac{1296}{1369}+\frac{12}{37}\times \frac{5625}{1369}\)
V(Y)\(=\frac{25 \times 1296}{50653}+\frac{12 \times 5625}{50653}\)
V(Y)\(=\frac{25 \times 1296 +12 \times 5625}{50653}\)
V(Y)\(=\frac{99900}{50653}\simeq1,97\)
\(\sigma(Y)=\sqrt{1,97}\simeq1,4\)
\([E(Y)-\sigma(Y) ;E(Y)+\sigma(Y)]\simeq[-0,027-1 ; -0,027+1]\simeq[-1,02 ; 0,98]\)
\(\color{red}{\textbf{On peut donc en déduire que les gains pour ce deuxième jeu sont moins dispersés car }}\)
\(\color{red}{[E(Y)-\sigma(Y) ;E(Y)+\sigma(Y)]\subset[E(X)-\sigma(X) ;E(X)+\sigma(X)].}\)
Question
\(\color{magenta}{\textbf{Partie C :}}\)
On note Z la variable aléatoire donnant le gain pour une mise de 1 € dans le cas où un joueur parie sur les numéros rouges.
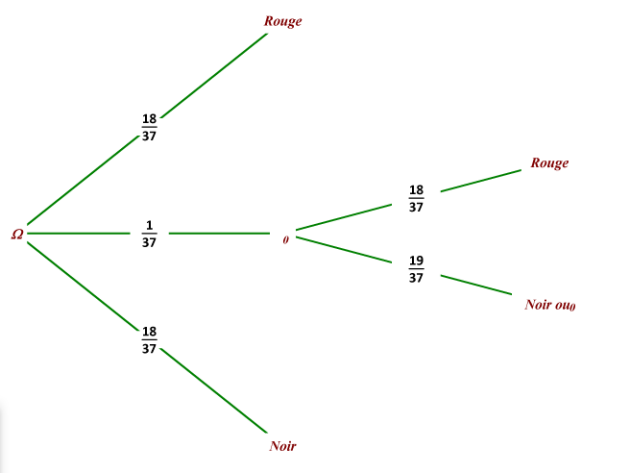
Dans ce cas, la règle concernant le numéro "0" est un peu différente.
Si le "0" sort, la mise est emprisonnée jusqu'au coup suivant.
Si celui-ci conduit à un numéro rouge, on ne gagne ni on ne perd.
Si c'est un numéro noir ou à nouveau le "0", l'euro est perdu.
a. Écrire la loi de probabilité de la variable aléatoire Z.
b. Calculer l'espérance de la variable aléatoire Z.
c. Calculer la variance et l'écart type de la variable aléatoire Z.
Solution
\(z_i\) | -1 | 0 | 1 |
|---|---|---|---|
\(p(Z=z_i)\) | \(\frac{18}{37}\)+\(\frac{1}{37}\times \)\(\frac{18}{37}=\frac{18+18\times 37}{37^2}=\frac{684}{1369}\) | \(\frac{1}{37}\times \)\(\frac{19}{37}=\frac{19}{37^2}=\frac{19}{1369}\) | \(\frac{18}{37}\) |
\(\frac{684}{1369}+\frac{19}{1369}+\frac{18}{37}=\frac{684}{1369}+\frac{19}{1369}+\frac{666}{37}=1\)
E(Z)=\(\frac{684}{1369}\times (-1)+\frac{19}{1369}\times 0+\frac{18}{37}\times 1\)
\(E(Z)=\frac{-684}{1369}+\frac{666}{37}\)
\(E(Z)=\frac{-18}{1369}\simeq-0,013\)
\(\color{red}{E(Z)<E(X)=E(Y)}\)
\(\color{red}{\textbf{On perd donc en moyenne moins d'argent pour un grand nombre de jeu avec ce troisième jeu. }}\)
V(Z)=\(\frac{684}{1369}\times (-1-(\frac{-18}{1369}))^2+\frac{19}{1369}\times (0-\frac{-18}{1369})^2+\frac{18}{37}\times (1-\frac{-18}{1369})^2\)
V(Z)=\(\frac{684}{1369}\times (-1+\frac{18}{1369}))^2+\frac{19}{1369}\times (\frac{18}{1369})^2+\frac{18}{37}\times (1+\frac{18}{1369})^2\)
V(Z)=\(\frac{684}{1369}\times (-\frac{1369}{1369}+\frac{18}{1369}))^2+\frac{19}{1369}\times (\frac{18}{1369})^2+\frac{18}{37}\times (\frac{1369}{1369}+\frac{18}{1369})^2\)
V(Z)=\(\frac{684}{1369}\times (-\frac{1351}{1369}))^2+\frac{19}{1369}\times (\frac{18}{1369})^2+\frac{18}{37}\times (\frac{1387}{1369})^2\)
V(Z)=\(\frac{684}{1369}\times \frac{1 825 201}{1 874 161}+\frac{19}{1369}\times \frac{324}{1 874 161}+\frac{18}{37}\times \frac{1 923 769}{1 874 161}\)
V(Z)=\(\frac{684}{1369}\times \frac{1 825 201}{1 874 161}+\frac{19}{1369}\times \frac{324}{1 874 161}+\frac{18}{37}\times \frac{1 923 769}{1 874 161}\)
V(Z)=\(\frac{684 \times 1 825 201 +19 \times 324 +18 \times 1 923 769}{1369 \times 1 874 161}\)
V(Z)=\(\frac{1283071482}{2565726409}\simeq5\)
\(\sigma(Z)=\sqrt{5}\simeq2,23\)
\([E(Z)-\sigma(Z) ;E(Z)+\sigma(Z)]\simeq[-0,013-2,23 ; -0,013+2,23]\simeq[-2,22 ;2,22]\)