Exercice : Yaourt Deschamps
Monsieur Deschamps fabrique des yaourts qu'il commercialise sous la marque « Yaourts Des Champs ».
Il fait distribuer des prospectus publicitaires dans les boîtes à lettres et il estime qu'après la distribution de x milliers de prospectus, la probabilité qu'une personne connaisse les « Yaourts Des Champs » s'exprime par la fonction
f définie par :
\(f(x)=\frac{4x + 1}{5x + 5}\) où \(x\) appartient à l'intervalle [0 ; 11].

Question
1. a. Déterminer \(f'(x).\)
Solution
\(f(x)=\frac{4x + 1}{5x + 5}\)
\(f(x)=\frac{u}{v}\)
\(f'(x)=\frac{u'v-uv'}{v^2}\)
\(\begin{cases}u=4x+1\\v=5x+5\end{cases}\)
\(\begin{cases}u'=4\\v'=5\end{cases}\)
\(f'(x)=\frac{4(5x+5)-5(4x+1)}{(5x+5)^2}\)
\(f'(x)=\frac{20x+20-20x-5}{(5x+5)^2}\)
\(f'(x)=\frac{15}{(5x+5)^2}=\frac{15}{25x^2+25x+25)}=\color{red}{\frac{3}{5x^2+5x+5}}\)
\(f'(x)>0\)
Question
b. En déduire le tableau de variations de f.
Solution

Donc si l'entreprise distribue aucun prospectus, 20% de la population connaît la marque.
Si l'entreprise distribue 11 mille prospectus, 75% de la population connaît la marque.
Question
c) Compléter le tableau de valeurs de la fonction \(f\) de 0 à 11
\(x\) | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
\(f(x)\) |
Solution
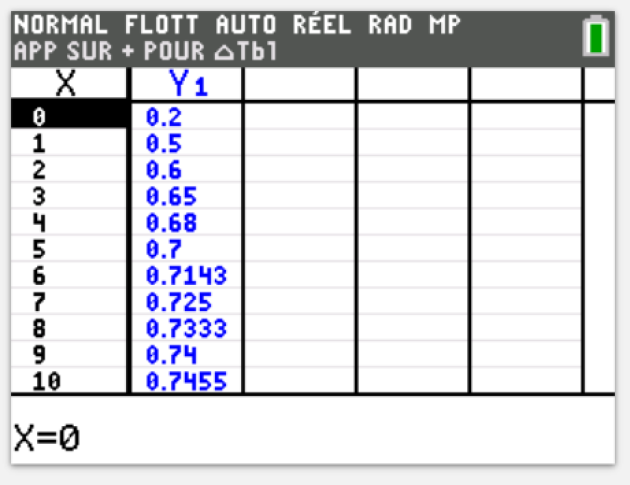
\(x\) | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
\(f(x)\) | 0,2 | 0,5 | 0 ,6 | 0,65 | 0,68 | 0,7 | 0,7143 | 0,725 | 0,733 | 0,74 | 0,7455 | 0 ,75 |
Question
2. a.Grâce à la question précédente, déterminer le nombre de prospectus qu'il faut distribuer pour que la probabilité qu'une personne connaisse les « Yaourts Des Champs » soit égale à 0,7(70%) puis 0,75(75%).
Solution
Le nombre de prospectus qu'il faut distribuer pour que la probabilité qu'une personne connaisse les « Yaourts Des Champs » soit égale à 0,7 est 5 000
Le nombre de prospectus qu'il faut distribuer pour que la probabilité qu'une personne connaisse les « Yaourts Des Champs » soit égale à 0,75 est 11 000
Question
b. En déduire le nombre de prospectus supplémentaires qu'il faut distribuer pour que la probabilité qu'une personne connaisse les « Yaourts Des Champs »
passe de 0,7 à 0,75.
Monsieur Deschamps décide de ne faire distribuer que 5 000 prospectus.
Expliquer son choix.
Solution
Il faut donc vendre 6 000 prospectus supplémentaires pour que la probabilité qu'une personne connaisse les « Yaourts Des Champs »
passe de 0,7 à 0,75.(11 000- 5 000=6 000)
\(\color{red}{\textbf{Monsieur Deschamps peut penser que le nombre de prospectus supplémentaires à commander n'augmentera pas suffisamment les ventes.}}\)