Exercice : Deux dés
Un dé à 6 faces est truqué de la façon suivante :
chaque numéro pair a deux fois plus de chance de sortir qu'un numéro impair.
Question
1. Calculer la probabilité de l'évènement « obtenir un 6 »
Solution
p : probabilité d'un numéro impair.
p("obtenir 1")+p("obtenir 2")+p("obtenir 3")+p("obtenir 4")+p("obtenir 5")+p("obtenir 6")=1
p+2p+p+2p+p+2p=1
9p=1
\(p=\frac{1}{9}\)
d'où le tableau de loi de probabilité
Face | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
probabilité | \(\frac{1}{9}\) | \(\frac{2}{9}\) | \(\frac{1}{9}\) | \(\frac{2}{9}\) | \(\frac{1}{9}\) | \(\frac{2}{9}\) |
Question
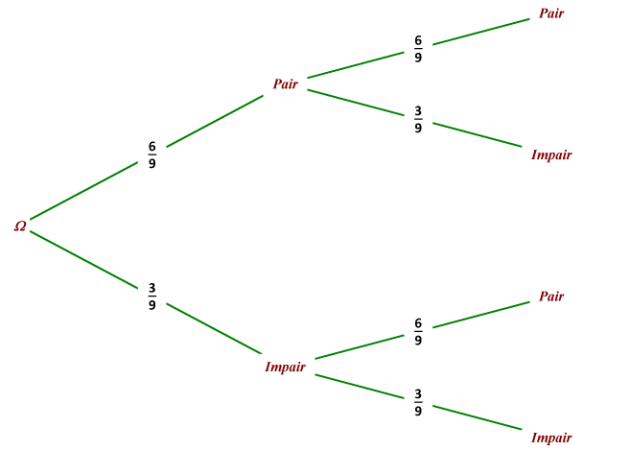
2. On lance deux fois le dé.
a. Calculer la probabilité d'obtenir deux fois un numéro pair.
Solution
\(p("obtenir deux numéros pairs")=\frac{6}{9}\times \frac{6}{9}=\frac{36}{81}\)
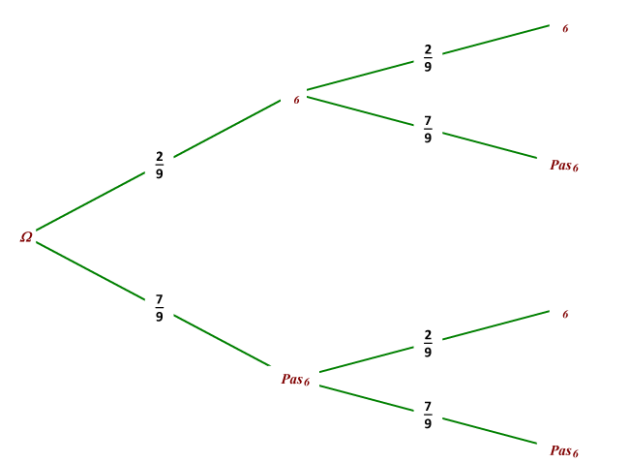
Question
b. Calculer la probabilité d'obtenir deux fois un 6.
Solution
\(p("obtenir deux 6")=\frac{2}{9}\times \frac{2}{9}=\frac{4}{81}\)
Question
c. Calculer l'espérance du nombre de points obtenus dans le cas du lancé de deux dés
Solution
Face | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
probabilité | \(\frac{1}{9}\) | \(\frac{2}{9}\) | \(\frac{1}{9}\) | \(\frac{2}{9}\) | \(\frac{1}{9}\) | \(\frac{2}{9}\) |
2 :1+1 \(\mapsto \frac{1}{9} \times \frac{1}{9}=\frac{1}{81}\)
3 :1+2 ;2+1\(\mapsto \frac{1}{9} \times \frac{2}{9}+\frac{2}{9} \times \frac{1}{9}=\frac{4}{81}\)
4 :1+3 ;2+2 ;3+1\(\mapsto \frac{1}{9} \times \frac{1}{9}+\frac{2}{9} \times \frac{2}{9}+\frac{1}{9} \times \frac{1}{9}=\frac{6}{81}\)
5 :1+4 ;2+3 ;3+2 ;4+1\(\mapsto \frac{1}{9} \times \frac{2}{9}+\frac{2}{9} \times \frac{1}{9}+\frac{1}{9} \times \frac{2}{9}+\frac{2}{9} \times \frac{1}{9}=\frac{8}{81}\)
6 :1+5 ;2+4 ;3+3 ;4+2 ;5+1 \(\mapsto \frac{11}{81}\)
7 :1+6 ;2+5 ;3+4 ;4+3 ;5+2 ;6+1\(\mapsto \frac{12}{81}\)
8 :2+6 ;3+5 ;4+4 ;5+3 ;6+2\(\mapsto \frac{14}{81}\)
9 :3+6 ;4+5 ;5+4 ;6+3\(\mapsto \frac{8}{81}1\)
10 :4+6 ;5+5 ;6+4 \(\mapsto \frac{9}{81}\)
11 :5+6 ;6+5\(\mapsto \frac{4}{81}\)
12 :6+6\(\mapsto \frac{4}{81}\)
\(\frac{1}{81}+\frac{4}{81}+\frac{6}{81}+\frac{8}{81}+\frac{11}{81}+\frac{12}{81}+\frac{14}{81}+\frac{8}{81}+\frac{9}{81}+\frac{4}{81}+\frac{4}{81}\)
=\(\frac{1+4+6+ 8 +11 +12 + 14+ 8 +9+ 4 +4}{81}\)
=1
\(x_i\) | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|---|---|---|---|---|---|---|---|---|---|---|---|
\(p(X=x_i)\) | \(\frac{1}{81}\) | \(\frac{4}{81}\) | \(\frac{6}{81}\) | \(\frac{8}{81}\) | \(\frac{11}{81}\) | \(\frac{12}{81}\) | \(\frac{14}{81}\) | \(\frac{8}{81}\) | \(\frac{9}{81}\) | \(\frac{4}{81}\) | \(\frac{4}{81}\) |
\(E(X)=\frac{1}{81}\times 2 +\frac{4}{81} \times 3 + \frac{6}{81} \times 4 +\frac{8}{81} \times 5 +\frac{11}{81} \times 6 +\frac{12}{81} \times 7 +\frac{14}{81} \times 8 +\frac{8}{81} \times 9 +\frac{9}{81} \times 10+\frac{4}{81} \times 11 +\frac{4}{81} \times 12\)
\(E(X)=\frac{2}{81}+\frac{12}{81} + \frac{24}{81} +\frac{40}{81}+\frac{66}{81} +\frac{84}{81} +\frac{112}{81}+\frac{72}{81} +\frac{90}{81} +\frac{44}{81} +\frac{48}{81}\)
\(E(X)=\frac{2+12+24+40+66+84+112+72+90+44+48}{81}\)
\(E(X)=\frac{594}{81}=\frac{22}{3}\simeq7\)
Le nombre de points que l'on peut espérer obtenir est donc de \(\frac{22}{3}\simeq7\)