Exercice : N dés
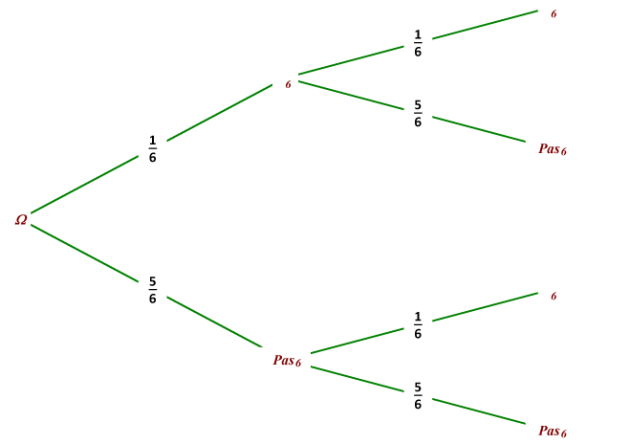
On lance n dés.
On note A l'événement « obtenir au moins un 6 ».
Question
1.Décrire l'événement \(\overline{A}\)
Solution
\(\overline{A}\) est l'évènement "obtenir aucun 6"
Question
2.Exprimer en fonction de n la probabilité p(\(\overline{A}\))
Question
3.En déduire que p(A) = \(1−(\frac{5}{6})^n\)
Solution
\(p(A)=p(\overline{\overline{A}})=1-p(\overline{A})=1-(\frac{5}{6})^n\)
Question
4.Compléter le tableau suivant :
n | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
\(p(A)\) |
Solution
n | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
\(p(A)\) | \(1-\frac{5}{6}=\frac{1}{6}\) | \(1-(\frac{5}{6})^2=1-\frac{25}{36}=\frac{11}{36}\) | \(1-(\frac{5}{6})^3=1-\frac{125}{216}=\frac{91}{216}\) | \(1-(\frac{5}{6})^4=1-\frac{625}{1296}=\frac{671}{1296}\) |
Question
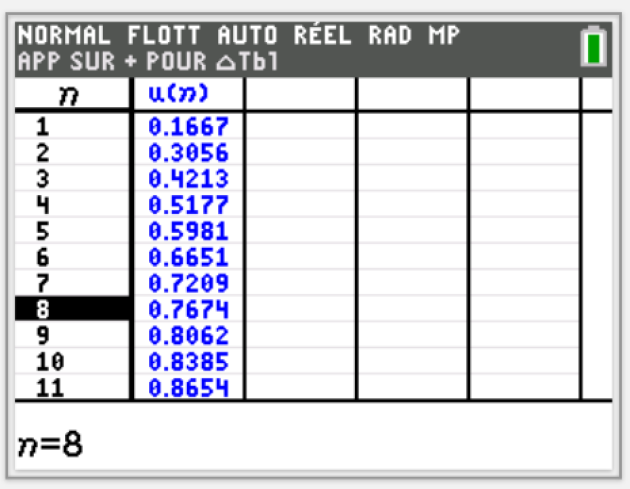
5.Combien de dés faut-il lancer pour que la probabilité d'obtenir au moins un six soit supérieure à \(\frac{3}{4}\) ?