Exercice : Fête Village
Le Comité des fêtes d'un village organise une loterie à l'aide de deux urnes.
L'urne \(U_1\) contient :
trois boules rouges notées \(R_1\), \(R_2\), \(R_3\) qui font gagner 2€
deux boules jaunes notées \(J_1\), \(J_2\) qui font gagner 3€.
L'urne \(U_2\) contient :
quatre boules bleues notées \(B_1\), \(B_2\), \(B_3\), \(B_4\) qui font gagner 1€
une boule verte V qui fait gagner 5€.
Pour participer à cette loterie, un joueur doit d'abord miser 5 €, puis tirer au hasard une boule dans chacune des deux urnes.
Les boules sont indiscernables au toucher.
On suppose que tous les tirages de couples de boules sont équiprobables.

Question
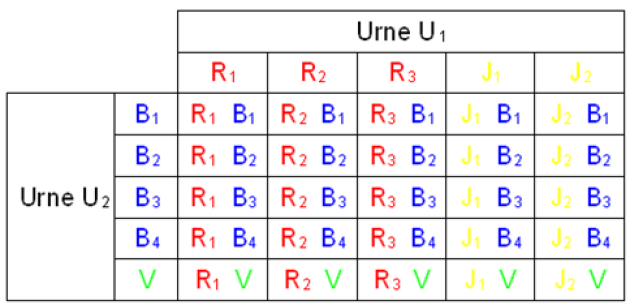
1. A l'aide d'un tableau ou d'un arbre montrer qu'il y a 25 couples de boules possibles.
Question
2. À chaque tirage de 2 boules la variable aléatoire X associe le gain réalisé par le joueur.
a. Déterminer l'ensemble des valeurs prises par la variable aléatoire X.
Solution
1 Boule Rouge + 1 Boule Bleue \(\mapsto 2+1-5=3-5=-2€\)
1 Boule Rouge + 1 Boule Verte \(\mapsto 2+5-5=7-5=2€\)
1 Boule Jaune + 1 Boule Verte \(\mapsto 3+5-5=3€\)
1 Boule Jaune + 1 Boule Bleue \(\mapsto 3+1-5=-1€\)
L'ensemble des valeurs prises par la variable aléatoire est {-2 ;-1 ;2 ;3}
Question
b. Présenter en tableau la loi de probabilité de la variable aléatoire X.
Solution
\(x_i\) | -2 | -1 | 2 | 3 |
|---|---|---|---|---|
\(p(X=x_i)\) | \(\frac{12}{25}\) | \(\frac{8}{25}\) | \(\frac{3}{25}\) | \(\frac{2}{25}\) |
Question
3. a. Calculer l'espérance mathématique E(X) de la variable aléatoire X.
Solution
\(E(X)=\frac{12}{25} \times (-2)+\frac{12}{25} \times (-1)+\frac{3}{25} \times 2 +\frac{2}{25} \times 3\)
\(E(X)=\frac{-24}{25}+\frac{-12}{25}+\frac{6}{25} +\frac{6}{25}\)
\(E(X)=\frac{-24}{25}\simeq-0,96\)
\(\color{red}{\textbf{Donc en moyenne le joueur perd 0,96€}}\)