Exemple 6
Un forain propose le jeu suivant :
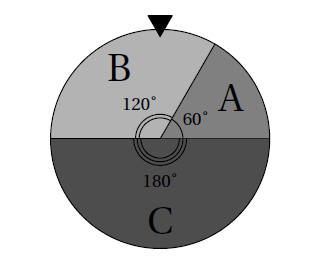
Le joueur fait tourner une roue divisée en secteurs de mesures 60°, 120° et 180° puis il lance un dé équilibré.
– Si la roue s'arrête sur le secteur A et s'il fait 6 avec le dé, il gagne un gros lot.
– Si la roue s'arrête sur le secteur B et s'il fait un nombre impair avec le dé, il gagne un petit lot.
– Dans les autres cas, il ne gagne rien.
Question
1. Modéliser cette expérience par un arbre pondéré.
2. En déduire la probabilité de chacun des événements suivants :
Question
a.« Le joueur gagne un gros lot » ;
Solution
\(p(« Le joueur gagne un gros lot » )=\frac{60}{360}\times \frac{1}{6}\)
\(\iff p(« Le joueur gagne un gros lot » )=\frac{1}{6}\times \frac{1}{6}\)
\(\iff p(« Le joueur gagne un gros lot » )=\frac{1}{36}\)
Question
b . « Le joueur gagne un lot (petit ou gros) » ;
Solution
p(« Le joueur gagne un lot (petit ou gros) »)
=p(« Le joueur gagne un gros lot » )+p(« Le joueur gagne un petit lot » )
\(=\frac{1}{36}+\frac{120}{360}\times \frac{3}{6}\)
\(=\frac{1}{36}+\frac{1}{3}\times \frac{1}{2}\)
\(=\frac{1}{36}+\frac{1}{6}\)
\(=\frac{1}{36}+\frac{6}{36}\)
\(=\frac{7}{36}\)
Question
c. « Le joueur ne gagne rien ».
Solution
p(« Le joueur ne gagne rien »)
\(=p(\overline{« Le joueur gagne un lot (petit ou gros) »})\)
\(=1-p(« Le joueur gagne un lot (petit ou gros) »)\)
\(=1-\frac{7}{36}\)
\(=\frac{36}{36}-\frac{7}{36}\)
\(=\frac{29}{36}\)