Exemple 8
On suppose que lorsqu'un couple attend un enfant, il est équiprobable d'avoir une fille ou un garçon.
Question
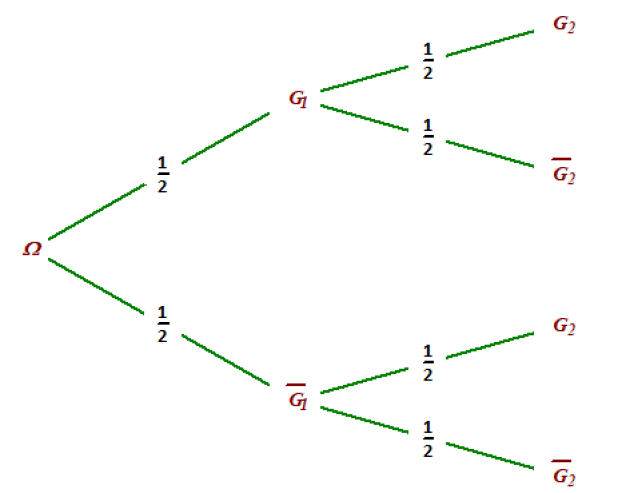
a.Représenter, à l'aide d'un arbre, les possibilités pour une famille de deux enfants.
Question
b.Quelle est la probabilité d'avoir deux garçons ?
Solution
\(p((G,G))=\frac{1}{2} \times \frac{1}{2}=\frac{1}{4}\)
Question
c.Quelle est la probabilité d'avoir une fille en second ?
Solution
\(p((G,D))+p((D,D))=\frac{1}{2} \times \frac{1}{2}+\frac{1}{2} \times \frac{1}{2}=\frac{1}{4}+\frac{1}{4}\)