Exercice : Exemple 8 :Jeu de 32 cartes
On considère l'expérience aléatoire suivante :

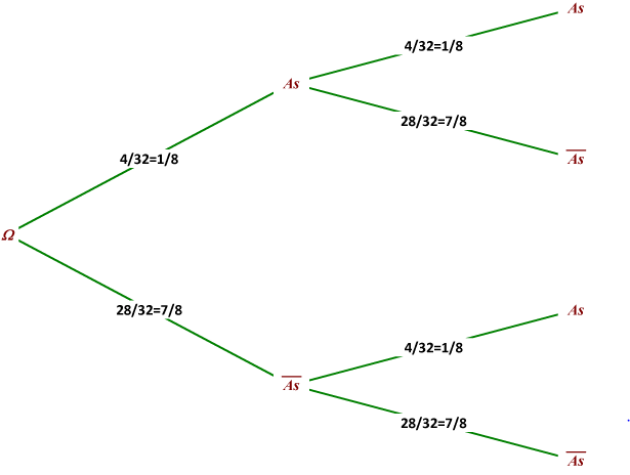
1.On tire une carte dans un jeu de 32 cartes deux fois de suite \(\color{red}{\text{avec remise}}\) (après le premier tirage la carte est remise dans le paquet).
Question
a. Soit E l'évènement : « On tire successivement deux as ».
Réaliser un arbre de probabilité pour cet événement dans le cas ou il y remise.
Question
b.Quelle est la probabilité que l’événement E se réalise ?
Solution
\(p(E)=p(\textbf{"tirer deux as"})=\frac{1}{8}\times \frac{1}{8}=\frac{1}{64}\)
Question
c.Quelle est la probabilité de l'évènement "On tire un as puis une carte qui n'est pas un as" ?
Solution
\(p(\textbf{"On tire un as puis une carte qui n'est pas un as"})=\frac{1}{8}\times \frac{7}{8}=\frac{7}{64}\)
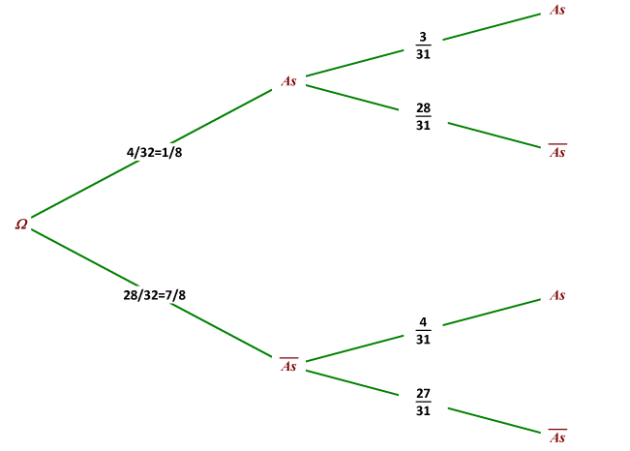
2.On tire une carte dans un jeu de 32 cartes deux fois de suite \(\color{red}{\text{sans remise}}\)
(après le premier tirage la carte n'est pas remise dans le paquet).
Question
a. Soit E l'évènement : « On tire successivement deux as ».
Réaliser un arbre de probabilité pour cet événement dans le cas ou il n'y a pas remise.
Question
b.Quelle est la probabilité que l’événement E se réalise ?
Solution
\(p(E)=p(\textbf{"tirer deux as"})=\frac{1}{8}\times \frac{3}{31}=\frac{3}{248}\)
Question
c.Quelle est la probabilité de l'évènement "On tire un as puis une carte qui n'est pas un as" ?
Solution
\(p(\textbf{"On tire un as puis une carte qui n'est pas un as"})=\frac{1}{8}\times \frac{28}{31}=\frac{28}{248}\)