Exercice : Exemple 15 :Pratiques Sportives
Une classe de seconde compte 28 élèves :
12 d'entre eux pratiquent la natation,
7 le volley-ball
13 ne pratiquent ni la natation, ni le volley-ball.
L'univers \(\Omega\) choisi est l'ensemble des élèves de la classe.
A l'événement “L'élève pratique le volley-ball” et B l'événement “L'élève pratique la natation”.
Question
1.Déterminer p(A) et p(B)
Solution
p(A)=\(p(“L'élève pratique le volley-ball”)=\frac{7}{28}=\frac{1}{4}\)
p(B)=\(p(“L'élève pratique la natation”)=\frac{12}{28}=\frac{3}{7}\)
Question
2.a. Interpréter \(\overline{A}∩\overline{B}\) et donner p(\(\overline{A}∩\overline{B}\)).
Solution
\(\overline{A}∩\overline{B}\)
L'élève ne pratique ni le volley-ball, ni la natation.
\(p( \overline{A}∩\overline{B})=\frac{13}{28}\)
Question
b. Calculer \(p(\overline{A})\) et \(p(\overline{B})\)
Solution
\(p( \overline{A})=1-p(A)=\)1-\(\frac{1}{4}=\)\(\frac{3}{4}\)
\(p( \overline{B})=1-p(B)=1-\frac{3}{7}=\frac{7}{7}-\frac{3}{7}=\frac{4}{7}\)
Question
c. Expliquer pourquoi \(\overline{(\overline{A}∩\overline{B} )}\) =A∪B
En déduire p(A∪B).
Solution
\(\overline{(\overline{A}∩\overline{B} )}\) est l'évènement contraire de l’événement "l'élève ne pratique ni le volley-ball, ni la natation" donc l'événement "l'élève pratique le volley-ball ou la natation".
il s'agit donc bien de A∪B.
\(p(A∪B)=p(\overline{(\overline{A}∩\overline{B} )})=1-p(\overline{A}∩\overline{B})=1-\frac{13}{28}=\frac{15}{28}\)
Il y a donc 13 élèves à l'extérieur et 15 élèves à l'intérieur des diagrammes
Soit \(n\) le nombre d'élèves pratiquants les deux sports (\(A \cap B\))
on a donc : \(12-n+7-n+n=15\)
soit \(19-n=15\)
donc \(n=4\)
On en déduit le diagramme suivant :
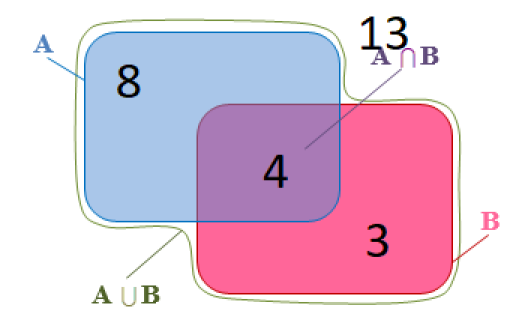
Calculer p(A∩B)
\(p(A \cup B)=p(A)+p(B)-p(A \cap B)\)
or \(\begin{cases} {p(A \cup B)=\frac{15}{28} \\p(A)=\frac{1}{4} \\p(B)=\frac{3}{7}} \end{cases}\)
donc
\(\frac{15}{28}=\frac{1}{4}+\frac{3}{7}-p(A \cap B)\)
\(\frac{15}{28}=\frac{7}{28}+\frac{12}{28}-p(A \cap B)\)
\(\frac{15}{28}=\frac{19}{28}-p(A \cap B)\)
\(\frac{15}{28}-\frac{19}{28}=-p(A \cap B)\)
\(p(A \cap B)=\frac{4}{28}\)
il y a donc 4 élèves qui pratiquent les deux sports (résultat qu'on avait déjà trouvé.)