Exercice : Exemple 10: Urne
Une urne contient 6 boules rouges, 7 boules vertes et 8 boules bleues.
On tire au hasard une boule de l'urne puis, sans la remettre dans l'urne, on en tire une seconde.
Un résultat de l'expérience est un couple de deux couleurs (par exemple (R,B)).
Question
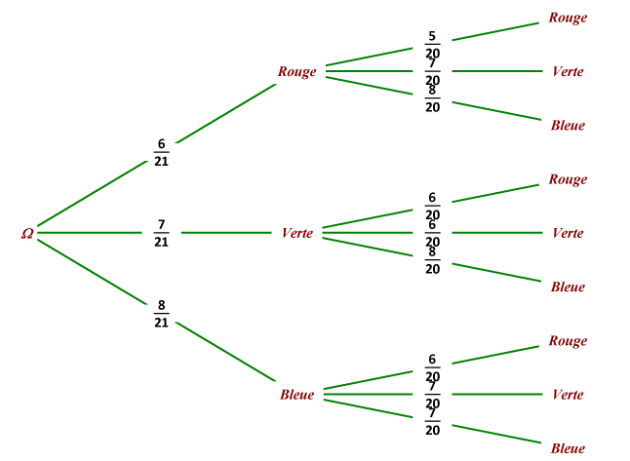
a.Représenter cette situation par un arbre pondéré.
Question
2. Calculer la probabilité des événements suivants :
E : «On obtient deux boules rouges. »
Solution
\(p((R,R))=\frac{6}{21} \times \frac{5}{20}\)
\(\iff p((R,R))=\frac{2}{7} \times \frac{1}{4}\)
\(\iff p((R,R))=\frac{2}{28}=\frac{1}{14}\)
Question
F : «On obtient au maximum une boule rouge. »
Solution
\(p("obtenir au maximum une boule rouge")=p(\overline{(R,R)})=1-p((R,R)=1-\frac{1}{14}\)
\(\iff p("obtenir au maximum une boule rouge")=p(\overline{(R,R)})=1-p((R,R)=\frac{14}{14}-\frac{1}{14}\)
\(\iff p("obtenir au maximum une boule rouge")=\frac{13}{14}\)
Question
G : «On obtient une boule bleue et une boule verte. »
Solution
p((B,V))+p((V,B))
\(=\frac{8}{21} \times \frac{7}{20}+\frac{7}{21} \times \frac{8}{20}\)
\(=\frac{8}{3} \times \frac{1}{20}+\frac{1}{3} \times \frac{2}{5}\)
\(=\frac{2}{3} \times \frac{1}{5}+\frac{1}{3} \times \frac{2}{5}\)
\(=\frac{2}{15}+\frac{2}{15}\)
\(=\frac{4}{15}\)