Exercice : Exemple 13 : Feu de Signalisation [Chapitre VIII Probabilités]

Exercice : Exemple 13 : Feu de Signalisation

Sur son trajet, un automobiliste rencontre successivement deux feux tricolores. Les deux feux sont réglés de la même façon :

à un instant donné, un feu est « au rouge » avec une probabilité de \(\frac{1}{4}\) , à l'orange avec une probabilité de \(\frac{1}{8}\) et « au vert » avec une probabilité de \(\frac{5}{8}\).

De plus, l'état de chaque feu lorsque l'automobiliste s'y présente est aléatoire, et ne dépend pas de l'état de l'autre feu.

Question

1.Préciser l'univers correspondant à la situation aléatoire étudiée.

Solution

\(\Omega=\{(V_1 ,V_2),(V_1 ,O_2),(V_1 ,R_2),(O_1 ,V_2),(O_1 ,O_2),(O_1 ,R_2),(R_1 ,V_2),(R_1 ,O_2),(R_1 ,R_2)\}\)

Question

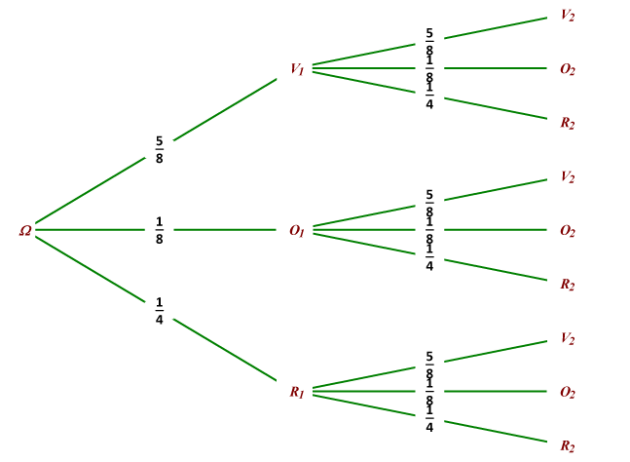
2.Mettre en place un arbre modélisant la situation et préciser la loi de probabilité correspondante.

Solution

Vérifions les valeurs données :

\(\frac{1}{8}+\frac{5}{8}+\frac{1}{4}=\frac{1}{8}+\frac{5}{8}+\frac{2}{8}=\frac{8}{8}=1\)

Issue	\((V_1 ,V_2)\)	\((V_1 ,O_2)\)	\((V_1 ,R_2)\)	\((O_1 ,V_2)\)	\((O_1 ,O_2)\)	\((O_1 ,R_2)\)	\((R_1 ,V_2)\)	\((R_1 ,O_2)\)	\((R_1 ,R_2)\)
p(Issue)	\(\frac{5}{8} \times \frac{5}{8} =\frac{25}{64}\)	\(\frac{5}{8} \times \frac{1}{8} =\frac{5}{64}\)	\(\frac{5}{8} \times \frac{1}{4} =\frac{5}{32}\)	\(\frac{1}{8} \times \frac{5}{8} =\frac{5}{64}\)	\(\frac{1}{8} \times \frac{1}{8} =\frac{1}{64}\)	\(\frac{1}{8} \times \frac{1}{4} =\frac{1}{32}\)	\(\frac{1}{4} \times \frac{5}{8} =\frac{5}{32}\)	\(\frac{1}{4} \times \frac{1}{8} =\frac{1}{32}\)	\(\frac{1}{4} \times \frac{1}{4} =\frac{1}{16}\)

3.Calculer la probabilité des événements :

Question

A : « L'automobiliste rencontre les deux feux au vert »

Solution

p(A)=p( « L'automobiliste rencontre les deux feux au vert »)\(=\frac{5}{8}\times\frac{5}{8}\)=\(\frac{25}{64}\)

Question

B : « l'automobiliste doit s'arrêter au moins une fois devant l'un des feux. »

On rappelle qu'on doit s'arrêter au feu rouge ainsi qu'au feu orange.

p(B)=p(« l'automobiliste doit s'arrêter au moins une fois devant l'un des feux. »)=\(\frac{5}{8} \times(\frac{1}{8}+\frac{1}{4})+\frac{1}{8}\times(\frac{5}{8}+\frac{1}{8}+\frac{1}{4})+\frac{1}{4}\times(\frac{5}{8}+\frac{1}{8}+\frac{1}{4})\)

\(p(B)=\frac{5}{8} \times(\frac{1}{8}+\frac{2}{8})+\frac{1}{8}+\frac{1}{4}\)

\(p(B)=\frac{5}{8} \times \frac{3}{8}+\frac{1}{8}+\frac{1}{4}\)

\(p(B)=\frac{15}{64}+\frac{1}{8}+\frac{2}{8}\)

\(p(B)=\frac{15}{64}+\frac{3}{8}\)

\(p(B)=\frac{15}{64}+\frac{24}{64}\)

\(p(B)=\frac{39}{64}\)

\(\color{magenta}{\text{Deuxième méthode de calcul :}}\)

p(B)=p(« l'automobiliste doit s'arrêter au moins une fois devant l'un des feux. »)=p(\(\overline{\textbf{« L'automobiliste rencontre les deux feux au vert. »}}\))

donc p(B)=\(1-p(A)=1-\frac{25}{64}=\frac{64}{64}-\frac{25}{64}=\frac{39}{64}\)