Exercice : Exercice d'introduction
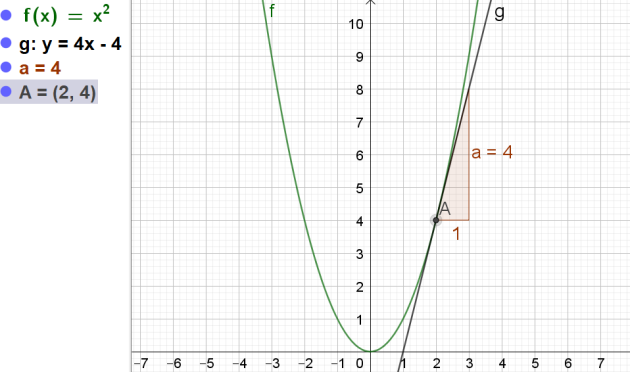
Soit la fonction \(f\) définie sur \(\mathbb{R}\) par\( f(x)=x^2\)
Question
1.Calculer le nombre dérivé de la fonction \(f\) en \(x=2\)
Solution
\(\frac{f(2+h)-f(2)}{(2+h)-2}\)
=\(\frac{(2+h)^2-2^2}{h}\)
\(= \frac{ (2+h)^2-4}{h}\)
\(= \frac{ 2^2+2\times 2 \times h+h^2-4}{h}\)
\(= \frac{ 4+4h+h^2-4}{h}\)
\(= \frac{ 4h+h^2}{h}\)
\(= \frac{ h(4+h)}{h}=4+h\)
\(f'(2)=lim_{h\mapsto 0}\frac{f(2+h)-f(2)}{h}\)
\(f'(2)=lim_{h\mapsto 0}(4+h)=4\)
donc \(f'(2)=4\)
Question
2.Déterminer l'équation de la tangente à la fonction \(f(x)=x^2\) au point d'abscisse 2
Solution
L'équation de la tangente au point d'abscisse 2 est donnée par la formule :
\(y=f'(a)(x-a)+f(a)\)
\(y=f'(2)(x-2)+f(2)\)
or \(f'(2)=4\) et \(f(2)=4\) d'après les calculs précédents.
\(\iff y=4(x-2)+4\)
\(\iff y=4(x-2)+4\)
\(\iff y=4x-8+4=4x-4\)
Question
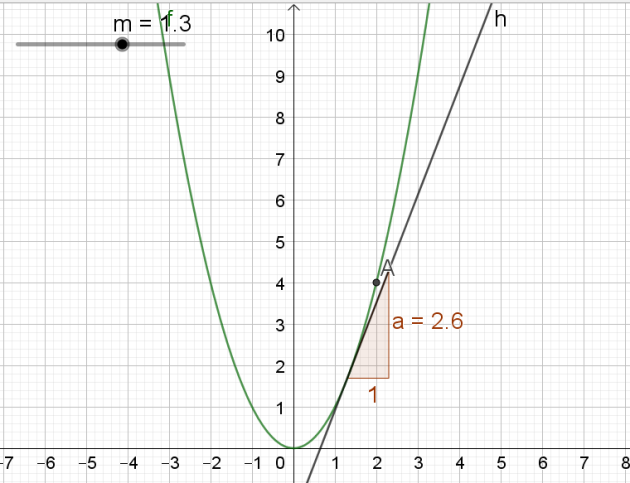
3.Calculer le nombre dérivé de la fonction \(f\) en un nombre quelconque \(a\).
Solution
Pour \(h \ne 0\) :
\(\frac{f(a+h)-f(a)}{(a+h)-a}\)
=\(\frac{(a+h)^2-a^2}{h}\)
\(= \frac{ a^2+2\times a \times h+h^2-a^2}{h}\)
\(= \frac{ a^2+2ah+h^2-a^2}{h}\)
\(= \frac{ 2ah+h^2}{h}\)
\(= \frac{ h(2a+h)}{h}=2a+h\)
\(f'(a)=lim_{h\mapsto 0}\frac{f(a+h)-f(a)}{h}\)
\(f'(a)=lim_{h\mapsto 0}(2a+h)=2a\)
donc \(f'(a)=2a\)
Pour tout nombre \(a\), on associe le nombre dérivé de la fonction \(f\) égal à \(2a\).
Ainsi, pour tout \(x\) de \(\mathbb{R}\), on a : \(f'(x)=2x\).
Question
Déterminer l'équation de la tangente à la fonction \(f(x)=x^2\) au point d'abscisse \(a\)
Solution
L'équation de la tangente au point d'abscisse \(a\) est donnée par la formule :
\(y=f'(a)(x-a)+f(a)\)
or \(f'(a)=2a\) et \(f(a)=a^2\) d'après les calculs précédents.
\(\iff y=2a(x-a)+a^2\)
\(\iff y=2a(x-a)+a^2\)
\(\iff y=2ax-2a^2+a^2=2ax-a^2\)