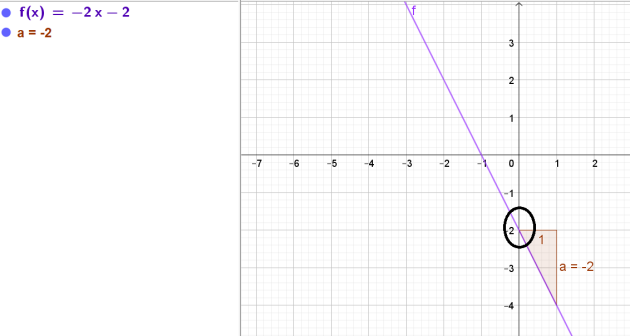
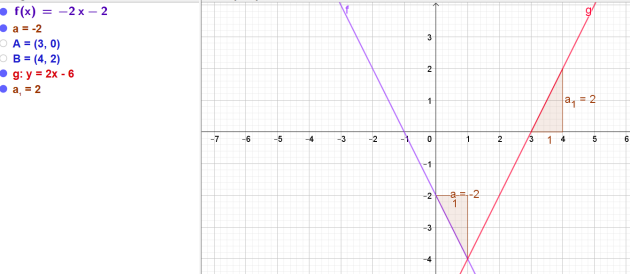
Exercice : Tangente 1
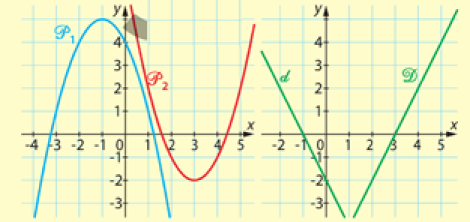
Parmi les quatre courbes ci-dessus:
- deux sont celles de deux fonctions.
- deux autres courbes sont celles de leurs fonctions dérivées.
Question
Les courbres \(P_1\) et \(P_2\) sont-elles celles des fonctions ou de leurs dérivées ?Justifier.
Donner les équations des deux fonctions permettant de définir les paraboles \(P_1\) et \(P_2\)
Solution
Les courbres \(P_1\) et \(P_2\) sont-elles celles des fonctions car
la dérivée d'une fonction du second degré :
\(f(x)=ax^2+bx+c\) est \(f'(x)=2ax+b\)
L'expression de \(f'\) est alors une fonction affine représentée par une droite.
Tandisque la dérivée d'une fonction affine est une fonction constante :
\(g(x)=mx+p\) est \(g'(x)=m\)
La forme canonique de la fonction permettant de définir la parabole \(P_1\) est :
\(f_1(x)=a(x-(-1))^2+5\) car le sommet de la parabole est le point (-1;5)
\(\iff f_1(x)=a(x+1)^2+5\)
La parabole passe par le point (0;4)
donc
\(f_1(0)=a(0+1)^2+5=4\)
\(\iff f_1(0)=a\times 1^2+5=4\)
\(\iff a+5=4\)
\(\iff a=4-5=-1\)
La forme canonique de la fonction permettant de définir la parabole \(P_1\) est donc :
\(f_1(x)=-1(x+1)^2+5=-(x+1)^2+5\)
La forme canonique de la fonction permettant de définir la parabole \(P_2\) est
\(f_2(x)=a(x-3)^2-2\) car le sommet de la parabole est le point (3;-2)
La parabole passe par le point (2;-1)
donc
\(f_2(2)=a(2-3)^2-2=-1\)
\(\iff f_2(2)=a\times (-1)^2-2=-1\)
\(\iff f_2(2)=a-2=-1\)
\(\iff a-2=-1\)
\(\iff a=-1+2\)
\(\iff a=1\)
La forme canonique de la fonction permettant de définir la parabole \(P_2\) est donc :
\(f_2(x)=(x-3)^2-2\)
Question
Donner les équations des deux fonctions permettant de définir les droites \((d)\) et \((\mathcal{D})\)
Solution
Equation de la droite \((d)\):\(y=-2x-2\)
Equation de la droite \((\mathcal{D})\) est de la forme :\(y=2x+b\)
La droite \((\mathcal{D})\) passe par le point (3;0)
donc \(0=2\times 3+b\)
\(\iff 0=6+b\)
\(\iff 6+b=0\)
\(\iff b=-6\)
L'équation de la droite \((\mathcal{D})\) est donc \(y=2x-6\)
Question
Associer aux fonctions définissant les paraboles \(P_1\) et \(P_2\)
leurs représentations graphiques parmi les droites \((d)\) et \((\mathcal{D})\)
Indice
\(u^n \mapsto nu^{n-1} \times u'\)
\(x \mapsto 1\)
\(u+v \mapsto u'+v'\)
\(k \mapsto 0\)
Solution
\(f'_1(x)=2(x-3)=2x-6 \mapsto (d)\)
\(f'_2(x)=-2(x+1)=-2x-2 \mapsto (\mathcal{D})\)