Exercice : Tangente 2
Pour chacune des fonctions suivantes définies sur \(\mathbb{R}\), déterminer l'équation de la tangente au point A dont on donne l'abscisse :
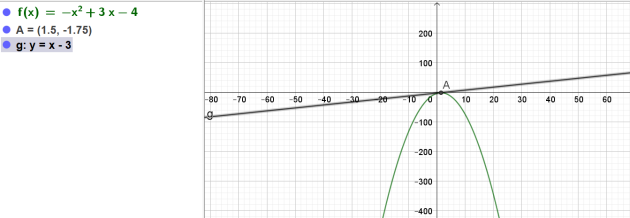
Question
1. \(f(x)=-x^2+3x-4\) en \(x_{A}= 1\)
Indice
\(x\mapsto 1\)
\(uv \mapsto u'v+uv'\)
\(k \mapsto 0\)
\(x^n \mapsto nx^{n-1}\)
\(ku \mapsto ku'\)
\(u+v\mapsto u'+v'\)
Solution
\(f'(x)=-2x+3\) en
\(f'(1)=-2 \times 1+3=1\)
\(f(1)=-1^2+3\times 1-4=-1+3-4=-2\)
L'équation de la tangente au point d'abscisse 1 est :
\(y=f'(1)(x-1)+f(1)\)
\(\iff y=1(x-1)-2\)
\(\iff y=1(x-1)-2\)
\(\iff y=x-1-2=x-3\)
Question
2. \(g(x)=-3-x+4x^2\) en \(x_{A}= -2\)
Indice
\(x\mapsto 1\)
\(uv \mapsto u'v+uv'\)
\(k \mapsto 0\)
\(x^n \mapsto nx^{n-1}\)
\(ku \mapsto ku'\)
\(u+v\mapsto u'+v'\)
Solution
\(g'(x)=-1+4\times 2x\)
\(\iff g'(x)=8x-1\)
\(\iff g'(-2)=8 \times (-2)-1=-17\)
\(g(-2)=-3-(-2)+4\times (-2)^2=-3+2+4 \times 4=15\)
L'équation de la tangente au point d'abscisse -2 est :
\(y=g'(-2)(x-(-2))+g(-2)\)
\(\iff y=-17(x+2)+15\)
\(\iff y=-17x-34+15\)
\(\iff y=-17x-19\)
Question
3. \(h(x)=4-5x^2\) en \(x_{A}= -3\)
Indice
\(x\mapsto 1\)
\(uv \mapsto u'v+uv'\)
\(k \mapsto 0\)
\(x^n \mapsto nx^{n-1}\)
\(ku \mapsto ku'\)
\(u+v\mapsto u'+v'\)
Solution
\(h'(x)=-5\times 2x\)
\(\iff h'(x)=-10x\)
\(h'(-3)=-10 \times (-3)=30\)
\(h(-3)=4-5\times (-3)^2=4-5\times 9=4-45=-41\)
L'équation de la tangente au point d'abscisse -3 est :
\(y=h'(-3)(x-(-3))+h(-3)\)
\(\iff y=30(x+3)-41\)
\(\iff y=30x+90-41\)
\(\iff y=30x+49\)
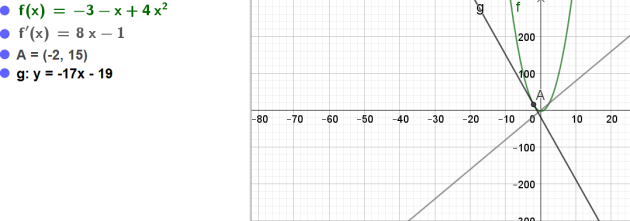
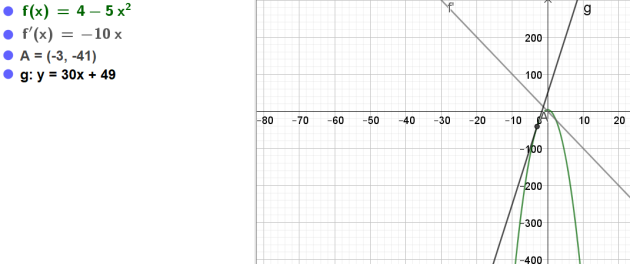
Question
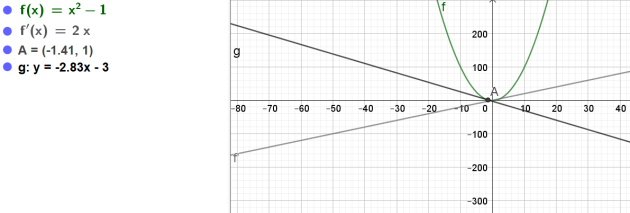
4. \(i(x)=x^2-1\) en \(x_{A}= -\sqrt{2}\)
Indice
\(x\mapsto 1\)
\(uv \mapsto u'v+uv'\)
\(k \mapsto 0\)
\(x^n \mapsto nx^{n-1}\)
\(ku \mapsto ku'\)
\(u+v\mapsto u'+v'\)
Solution
\(i'(x)=2x\)
\(i'(-\sqrt{2})=-2\sqrt{2}\)
\(i(-\sqrt{2})=(-\sqrt{2})^2-1=2-1=1\)
L'équation de la tangente au point d'abscisse \(-\sqrt{2}\) est :
\(y=i'(-\sqrt{2})(x-(-\sqrt{2}))+h(-\sqrt{2})\)
\(\iff y=-2\sqrt{2}(x+\sqrt{2}))+1\)
\(\iff y=-2\sqrt{2}x-2\sqrt{2}\times \sqrt{2}+1\)
\(\iff y=-2\sqrt{2}x- 2\sqrt{2} \times \sqrt{2}+1\)
\(\iff y=-2\sqrt{2}x-2 \times 2+1\)
\(\iff y=-2\sqrt{2}x-4+1\)
\(\iff y=-2\sqrt{2}x-3\)
Question
Une fonction \(j\) est telle que \(j( 2 ) =3\) et \(j'( 2 ) =5\)
On note A le point d'abscisse 2 de la courbe représentative \(C_{j}\) de la fonction \(j\) .
Donner l'équation réduite de la tangente à la courbe \(C_{j}\) au point A.
Solution
L'équation de la tangente au point d'abscisse 2 est :
\(y=j'(2)(x-2)+j(2)\)
\(\iff y=5(x-2)+3\)
\(\iff y=5x-10+3\)
\(\iff y=5x-7\)