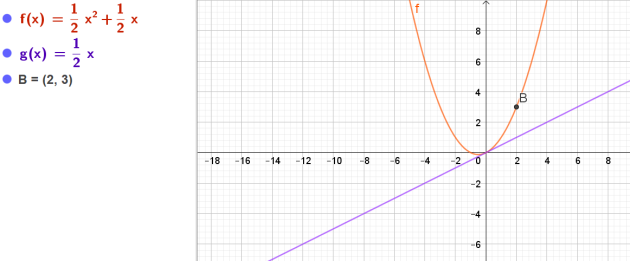
Exercice : Condition Courbe 1
\(f\) est une fonction définie sur \mathbb{R} par
\(f(x)=ax^2+bx+c\)
\(C_f\) est sa courbe représentative.
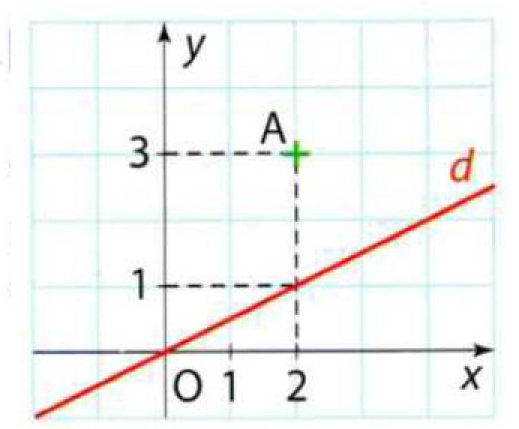
La droite (d) est tangente à la courbe \(C_f\) à l'origine O du repère
et \(C_f\) passe par le point A(2;3).
Question
1.a.Démontrer que \(f(0)=0\)
Solution
\(f(0)\) car la droite (d) est tangent à la courbe \(C_f\) en 0
Question
b.Démontrer que \(f'(0)=\frac{1}{2}\)
Solution
\(f'(0)=\frac{1}{2}\) car le coefficient directeur de la tangente en \(x=0\) est \(\frac{1}{2}\)
Question
c.\(f(2)=3\)
Solution
\(f(2)=3\) car la courbe \(C_f\) passe par le point A(2;3)
Question
2.Déduisez en la valeur de c ,b et a.
Solution
\(f(0)=0\)
\(\iff a \times 0^2+b \times 0+c=0\)
\(\iff c=0\)
L'équation de la fonction est donc de la forme \(f(x)=ax^2+bx\)
\(f'(0)=\frac{1}{2}\)
\(f'(x)=2ax+b\)
\(f'(0)=2a \times 0+b=\frac{1}{2}\)
\(\iff b=\frac{1}{2}\)
L'équation de la fonction est donc de la forme \(f(x)=ax^2+\frac{1}{2}x\)
\(f(2)=3\)
\(f(2)=a \times 2^2+\frac{1}{2}\times 2=3\)
\(\iff a \times 4+1=3\)
\(\iff a \times 4+1=3\)
\(\iff 4a+1=3\)
\(\iff 4a=2\)
\(\iff a=\frac{2}{4}=\frac{1}{2}\)
Question
3.Quelle est l'expression de \(f(x)\) ?
Solution
L'équation de la fonction est donc \(f(x)=\frac{1}{2}x^2+\frac{1}{2}x\)
