Exercice : Condition Courbe 4
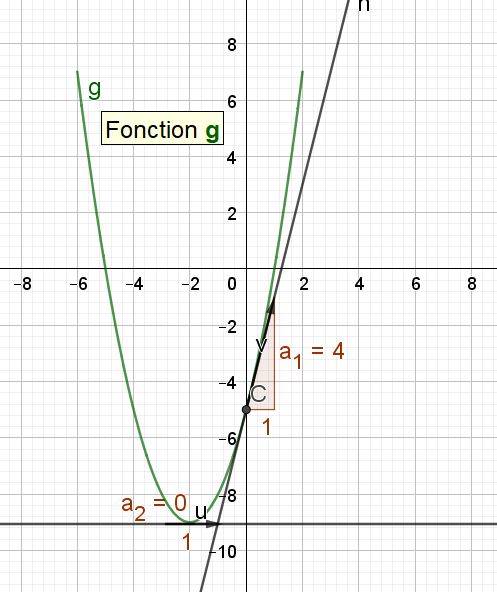
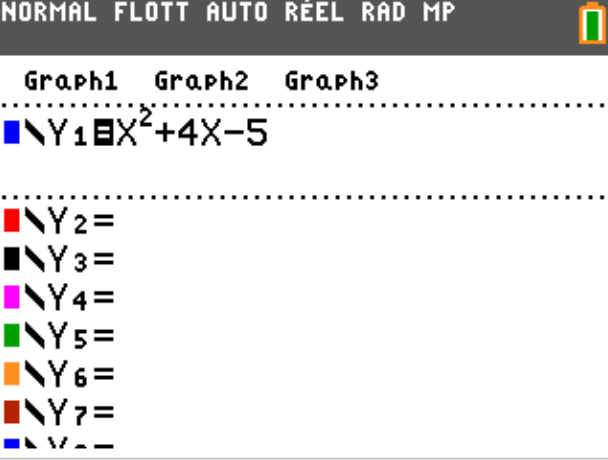
On appelle \(g\) la fonction définie par \(g(x) = x² + 4x -5.\) sur [-6;2]
Question
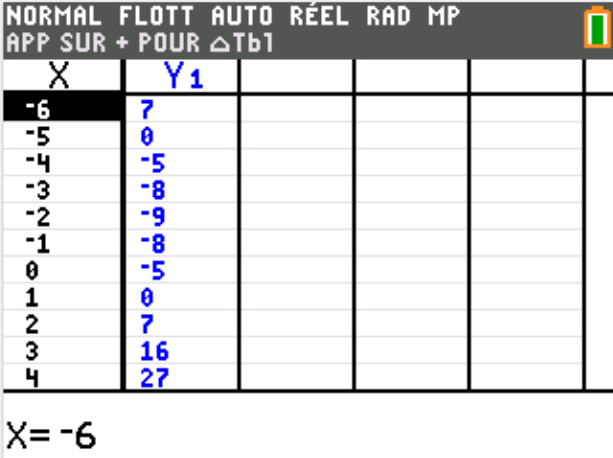
1. A l'aide du tableau que l'on complétera, tracer la courbe représentative de \(g\).
\(x\) | -6 | -5 | -4 | -3 | -2 | -1 | 0 | 1 | 2 |
|---|---|---|---|---|---|---|---|---|---|
\(g(x)\) |
Question
2. Donner l'expression de \(g'(x)\) la fonction dérivée de \(g\).
Solution
\(g'(x) = 2x + 4\times 1-0\)
\(\iff g'(x) = 2x + 4\)
Question
3. Déterminer \(g ‘(-2)\) et \(g ‘ (0)\) , puis tracer soigneusement les tangentes à \(C_g\) aux points d'abscisses -2 et 0.
Solution
\(g'(-2) = 2\times(-2)+ 4=-4+4=0\)
\(g'(0) = 2\times0+ 4=0+4=4\)