Exercice : Variations 1
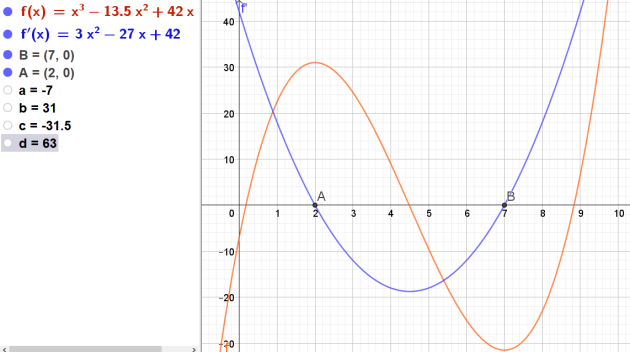
\(f\) est la fonction définie sur l'intervalle [0; 10] par : \(f(x) = x^3 - 13,5x^2 + 42x - 7\)
Question
1. Calculer la dérivée de \(f\)
Solution
\(f'(x) = 3x^2 - 13,5\times 2x + 42 \times 1- 0\)
\(\iff f'(x) = 3x^2 - 27x + 42\)
Question
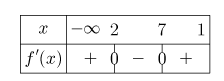
2. Dresser le tableau de signes de \(3x^2 - 27x + 42\)
Solution
\(\Delta=b^2-4ac=(-27)^2-4\times 3 \times 42\)
\(\iff \Delta=729-504=225\)
\(\begin{cases}x_1=\frac{-b-\sqrt{\Delta}}{2a}\\x_2=\frac{-b+\sqrt{\Delta}}{2a}\end{cases}\)
\(\iff \begin{cases}x_1=\frac{-(-27)-\sqrt{225}}{2\times 3}\\x_2=\frac{-(-27)+\sqrt{225}}{2\times 3}\end{cases}\)
\(\iff \begin{cases}x_1=\frac{27-15}{6}\\x_2=\frac{27+15}{6}\end{cases}\)
\(\iff \begin{cases}x_1=\frac{12}{6}\\x_2=\frac{42}{6}\end{cases}\)
\(\iff \begin{cases}x_1=2\\x_2=7\end{cases}\)
Question
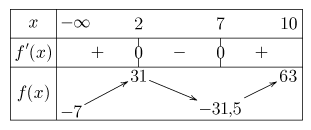
3. En déduire la tableau de variation de \(f\).