Exercice : Variations 4
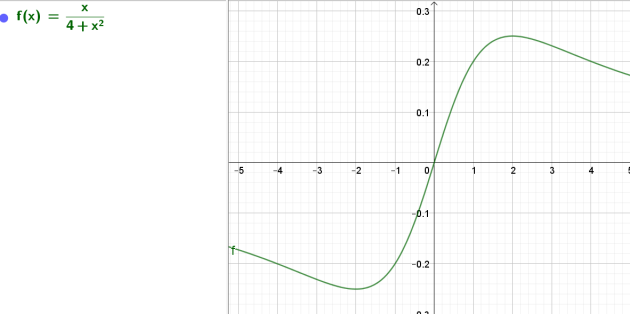
On appelle \(f\) la fonction définie par \(f(x)=\frac{x}{4+x^{2}}.\)
Question
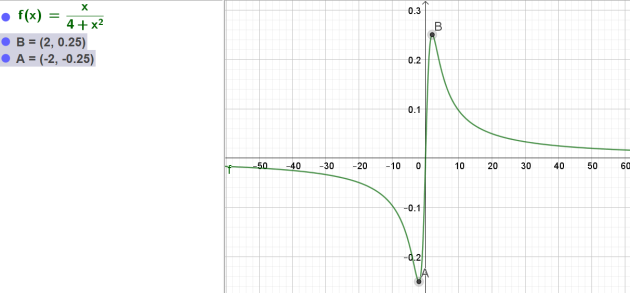
1.A l'aide de la calculatrice, conjecturer ses variations sur \(\mathbf{R}_{+}\).
Question
(b) Prouver que pour tous réels \(x_{1}\) et \(x_{2}\), \(f(x_{2})-f(x_{1})=\frac{(x_{2}-x_{1})(4-x_{1}x_{2})}{(1+x_{1}^{2})(1+x_{2}^{2})}\).
Solution
\(f(x_2)-f(x_1)=\frac{x_2}{4+x_2^{2}}-\frac{x_1}{4+x_1^{2}}\)
\(\iff f(x_2)-f(x_1)=\frac{x_2(4+x_1^{2})}{(4+x_2^{2})(4+x_1^{2})}-\frac{x_1(4+x_2^{2})}{(4+x_1^{2})((4+x_1^{2})}\)
\(\iff f(x_2)-f(x_1)=\frac{4x_2+x_2x_1^{2}-4x_1+x_1x_2^{2})}{(4+x_1^{2})((4+x_1^{2})}\)
\(\iff f(x_2)-f(x_1)=\frac{(x_{2}-x_{1})(4-x_{1}x_{2})}{(1+x_{1}^{2})(1+x_{2}^{2})}\)
Question
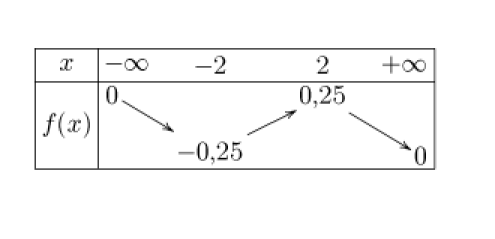
(c) En déduire les variations de \(f\) sur [0;2] puis sur \([2+\infty[.\)
Solution
Si \(0\le x_1 <x_2 \le2\)
\(x_2-x_1>0\)
\(0\lex_{1}x_{2}\le4\)
\(\Rightarrow 0\le4-x_{1}x_{2}\)
\(f(x_2)-f(x_1)=\frac{(x_{2}-x_{1})(4-x_{1}x_{2})}{(1+x_{1}^{2})(1+x_{2}^{2})}\ge 0\)
donc la fonction \(f\) est croissante sur [0;2].
Si \(2\le x_1 <x_2\)
\(x_2-x_1>0\)
\(4\lex_{1}x_{2}\)
\(\Rightarrow 4-x_{1}x_{2} \le 0\)
\(f(x_2)-f(x_1)=\frac{(x_{2}-x_{1})(4-x_{1}x_{2})}{(1+x_{1}^{2})(1+x_{2}^{2})}\le 0\)
donc la fonction \(f\) est décroissante sur [2 ;\infty[.