Exercice : Exercices d'applications du 2eme tableau
Déterminer les dérivées de fonctions suivantes ainsi que les ensembles de définitions :
Question
Question
Question
Question
Question
Question
Question
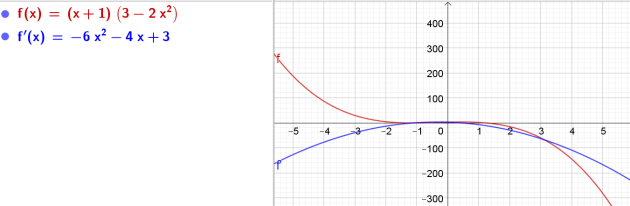
\(g(x)=(x+1)(3-2x^2)\)
Indice
\(ku \mapsto ku'\)
\(u+v \mapsto u'+v'\)
\(uv \mapsto u'v+uv'\)
\(k \mapsto 0\)
\(x^n \mapsto nx^{n-1}\)
Solution
\(g(x)=(x+1)(3-2x^2)\)
\(\begin{cases}u=x+1\\v=3-2x^2\end{cases}\)
\(\iff \begin{cases}u'=1\\v'=-2\times 2x\end{cases}\)
\(\iff \begin{cases}u'=1\\v'=-4x\end{cases}\)
\(g'(x)=1(3-2x^2)+(x+1)(-4x)\)
\(\iff g'(x)=3-2x^2+(x+1)(-4x)\)
\(\iff g'(x)=3-2x^2+(-4x)\times x+(-4x) \times 1\)
\(\iff g'(x)=3-2x^2-4x^2-4x\)
\(\iff g'(x)=-6x^2-4x+3\)
\(D_g=\mathbb{R}\) \(D_{g'}=\mathbb{R}\)
Question
Question
Question
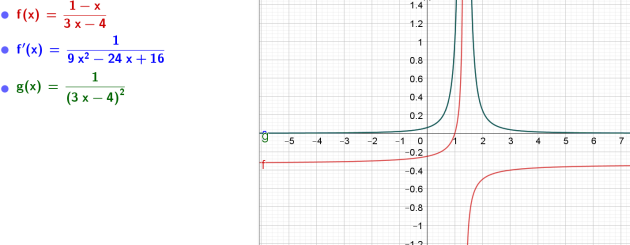
\(j(x)=\frac{1-x}{3x-4}\)
Indice
\(\frac{u}{v} \mapsto \frac{u'v-uv'}{v^2}\)
\(k \mapsto 0\)
\(u+v \mapsto u'+v'\)
\(ku \mapsto ku'\)
\(x \mapsto 1\)
Solution
\(\begin{cases}u=1-x\\v=3x-4\end{cases}\)
\(\iff \begin{cases}u'=-1\\v'=3\end{cases}\)
\(j'(x)=\frac{-1(3x-4)-(1-x)(3)}{(3x-4)^2}\)
\(\iff j'(x)=\frac{-3x+4-(3-3x)}{(3x-4)^2}\)
\(\iff j'(x)=\frac{-3x+4-3+3x}{(3x-4)^2}\)
\(\iff j'(x)=\frac{1}{(3x-4)^2}\)
\(3x-4=0\)
\(\iff 3x=4\)
\(\iff x=\frac{4}{3}\)
donc \(D_j=\mathbb{R}\backslash\{\frac{4}{3}\}\)\(D_{j'}=\mathbb{R}\backslash\{\frac{4}{3}\}\)
Question
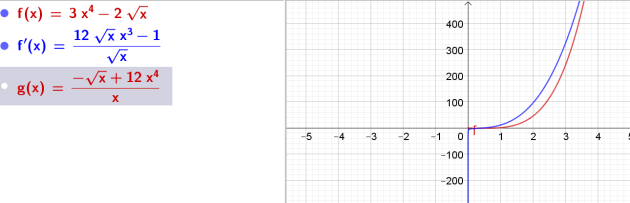
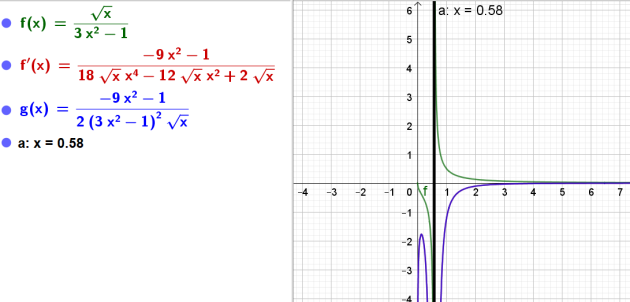
\(k(x)=\frac{\sqrt{x}}{3x^2-1}\)
Indice
\(\frac{u}{v} \mapsto \frac{u'v-uv'}{v^2}\)
\(k \mapsto 0\)
\(u+v \mapsto u'+v'\)
\(ku \mapsto ku'\)
\(x^2 \mapsto 2x\)
\(\sqrt{x} \mapsto \frac{1}{2\sqrt{x}}\)
Solution
\(\begin{cases}u=\sqrt{x}\\v=3x^2-1\end{cases}\)
\(\iff \begin{cases}u'=\frac{1}{2\sqrt{x}}\\v'=3\times 2x\end{cases}\)
\(\iff \begin{cases}u'=\frac{1}{2\sqrt{x}}\\v'=6x\end{cases}\)
\(k'(x)=\frac{\frac{1}{2\sqrt{x}} \times (3x^2-1) -\sqrt{x} \times 6x}{(3x^2-1)^2}\)
\(\iff k'(x)=\frac{1}{2\sqrt{x}} \times \frac{ (3x^2-1) -2 \sqrt{x} \times \sqrt{x} \times 6x}{(3x^2-1)^2}\)
\(\iff k'(x)=\frac{1}{2\sqrt{x}} \times \frac{ 3x^2-1 -2 x \times 6x}{(3x^2-1)^2}\)
\(\iff k'(x)=\frac{1}{2\sqrt{x}} \times \frac{ 3x^2-1 -12 x^2}{(3x^2-1)^2}\)
\(\iff k'(x)=\frac{ -9 x^2-1}{2\sqrt{x}(3x^2-1)^2}\)
\(\sqrt{x}\) existe \(si x\ge0\)
\(3x^2-1=0\)
\(\iff 3x^2=1\)
\(\iff x^2=\frac{1}{3}\)
\(\iff x_1=\frac{1}{\sqrt{3}} ou x_2=\frac{-1}{\sqrt{3}}\)
\(\iff x_1=\frac{\sqrt{3}}{\sqrt{3}^2} ou x_2=\frac{-\sqrt{3}}{\sqrt{3}^2}\)
\(\iff x_1=\frac{\sqrt{3}}{3} ou x_2=\frac{-\sqrt{3}}{3}\)
donc \(D_k=[0;+\infty[\backslash\{\frac{\sqrt{3}}{3}\}\)
\(D_{k'}=]0;+\infty[\backslash\{\frac{\sqrt{3}}{3}\}\)
Question
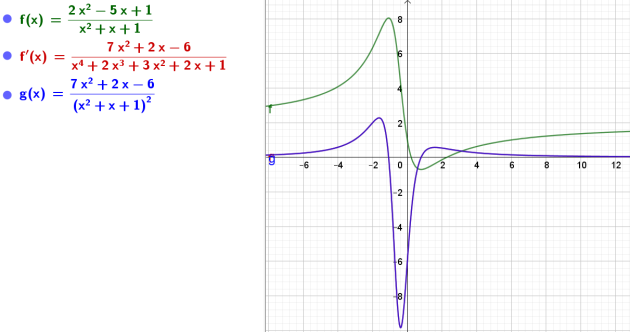
\(l(x)=\frac{2x^2-5x+1}{x^2+x+1}\)
Indice
\(\frac{u}{v} \mapsto \frac{u'v-uv'}{v^2}\)
\(k \mapsto 0\)
\(u+v \mapsto u'+v'\)
\(ku \mapsto ku'\)
\(x^n \mapsto nx^{n-1}\)
Solution
\(\begin{cases}u=2x^2-5x+1\\v=x^2+x+1\end{cases}\)
\(\iff \begin{cases}u'=4x-5\\v'=2x+1\end{cases}\)
\(l'(x)=\frac{(4x-5) \times (x^2+x+1) - (2x^2-5x+1)\times (2x+1)}{(x^2+x+1)^2}\)
\((4x-5) \times (x^2+x+1) =4x \times x^2 +4x \times x +4x \times 1 +(-5) \times x^2+ (-5) \times x +(-5) \times 1\)
\(\iff (4x-5) \times (x^2+x+1) =4x^3 +4x^2 +4x -5 x^2 -5 x -5\)
\(\iff (4x-5) \times (x^2+x+1) =4x^3 -x^2 -x -5\)
\((2x^2-5x+1)\times (2x+1)=2x^2 \times 2x +2x^2 \times (-5x)+2x^2 \times 1 +(-5x) \times 2x+(-5x) \times 1+ 1 \times 2x +1 \times 1\)
\(\iff (2x^2-5x+1)\times (2x+1)=4x^3 +2x^2-10x^2-5x+ 2x +1\)
\(\iff (2x^2-5x+1)\times (2x+1)=4x^3 -8x^2-3x +1\)
\((4x-5) \times (x^2+x+1) - (2x^2-5x+1)\times (2x+1)=(4x^3 -x^2 -x -5)-(4x^3 -8x^2-3x +1)\)
\(\iff (4x-5) \times (x^2+x+1) - (2x^2-5x+1)\times (2x+1)=4x^3 -x^2 -x -5-4x^3 +8x^2+3x -1\)
\(\iff (4x-5) \times (x^2+x+1) - (2x^2-5x+1)\times (2x+1)=7x^2+2x -6\)
\(l'(x)=\frac{7x^2+2x -6}{(x^2+x+1)^2}\)
\(x^2+x+1=0\)
\(\Delta=b^2-4ac=1^2-4\times 1 \times 1=1-4=-3\)
donc le dénominateur ne s’annule pas.
donc \(D_l=\mathbb{R}\)
\(D_{l'}=\mathbb{R}\)
Question
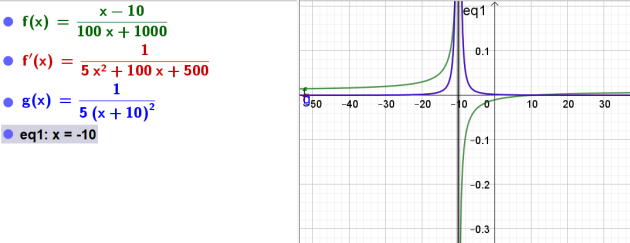
\(m(x)=\frac{x-10}{100x+1000}\)
Indice
\(\frac{u}{v} \mapsto \frac{u'v-uv'}{v^2}\)
\(k \mapsto 0\)
\(u+v \mapsto u'+v'\)
\(ku \mapsto ku'\)
\(x \mapsto 1\)
Solution
\(\begin{cases}u=x-10\\v=100x+1000\end{cases}\)
\(\iff \begin{cases}u'=1\\v'=100\end{cases}\)
\(m'(x)=\frac{1(100x+1000)-(x-10)\times 100}{(100x+1000)^2}\)
\(1(100x+1000)-(x-10)\times 100=100x+1000-(x\times 100-10\times 100)\)
\(\iff 1(100x+1000)-(x-10)\times 100=100x+1000-(100x-1000)\)
\(\iff 1(100x+1000)-(x-10)\times 100=100x+1000-100x+1000\)
\(\iff 1(100x+1000)-(x-10)\times 100=2000\)
\(m'(x)=\frac{2000}{(100x+1000)^2}\)
\(m'(x)=\frac{2000}{100^2(x+10)^2}\)
\(m'(x)=\frac{20}{100(x+10)^2}\)
\(m'(x)=\frac{1}{5(x+10)^2}\)
\(x+10=0\)
\(\iff x=-10\)
donc \(D_m=\mathbb{R}\backslash\{-10\}\)
\(D_{m'}=\mathbb{R}\backslash\{-10\}\)