Exercice : 3x^3+4x^2-6x+2
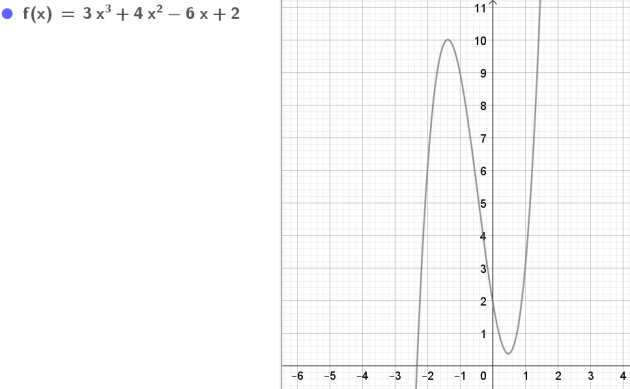
On appelle \(f\) la fonction définie sur \(\mathbb{R}\) par\( f( x )=3x³+4x²-6x+2.\)
Question
1. Calculer \(f(2)\) et \(f(-1).\)
Question
Question
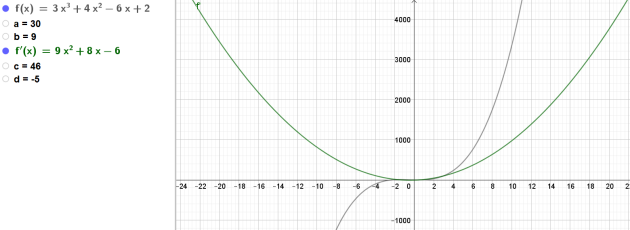
3. Donner les valeurs de \(f'(2)\) et \(f'(-1)\)
Question
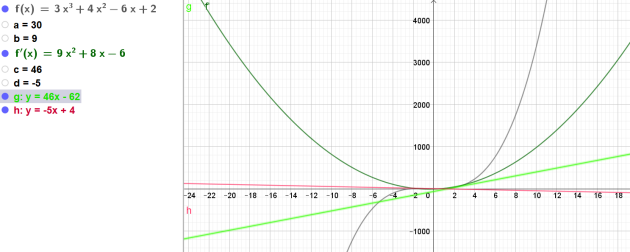
4. En déduire les équations des tangentes à la courbe de la fonction \(f\) en 2 et -1
Solution
Equation de la tangente au point d'abscisse \(x=2\):
\(y=f'(2)(x-2)+f(2)\)
\(\iff y=46(x-2)+30\)
\(\iff y=46x-92+30\)
\(\iff y=46x-62\)
L'équation de la tangente au point d'abscisse \(x=2\) est donc \(y=46x-62\)
Equation de la tangente à l'abscisse \(x=-1\):
\(y=f'(-1)(x-(-1))+f(-1)\)
\(\iff y=-5(x+1)+9\)
\(\iff y=-5x-5+9\)
\(\iff y=-5x+4\)
L'équation de la tangente au point d'abscisse \(x=-1\) est donc \(y=-5x+4\)