Exercice : (3x²+2)/(x+3)
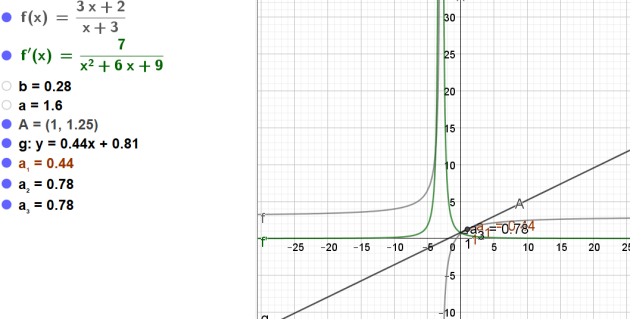
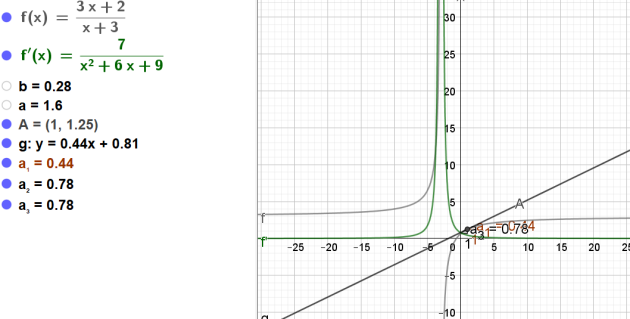
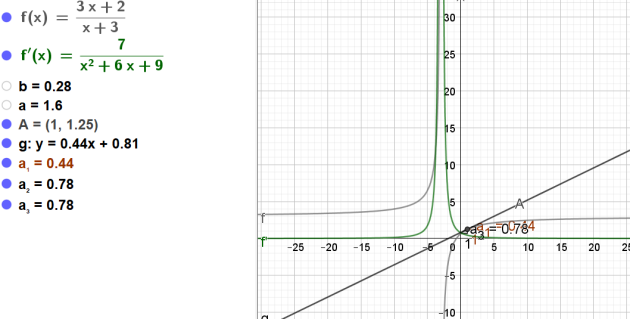
\(f\) est la fonction définie sur \(\mathbb{R}\) par \(f(x)=\frac{3x+2}{x+3}\)
Question
1. Calculer la dérivée \(f'\) de \(f\)
Indice
\(x\mapsto 1\)
\(\frac{u}{v} \mapsto \frac{u'v-uv'}{v^2}\)
\(ku \mapsto ku'\)
\(u+v\mapsto u'+v'\)
Solution
\(\begin{cases}u=3x+2\\v=x+3\end{cases}\)
\(\begin{cases}u'=3\\v'=1\end{cases}\)
\(f'(x)=\frac{3(x+3)-(3x+2)\times 1}{(x+3)^2}\)
\(\iff f'(x)=\frac{3x+9-3x-2}{(x+3)^2}\)
\(\iff f'(x)=\frac{7}{(x+3)^2}\)
Question
2.Quel est le coefficient directeur de la tangente à la courbe représentative
au point A d'abscisse 1 ?
Solution
\(f'(1)=\frac{7}{1^2+6\times 1+9}\)
\(\iff f'(1)=\frac{7}{1+6+9}\)
\(\iff f'(1)=\frac{7}{16}\)
L'équation de la tangente est donc \(y=\frac{7}{16}x+b\)
Question
3.Quelle est l'ordonnée du point A ?
Solution
\(f(1)=\frac{3 \times 1+2}{1+3}=\frac{5}{4}\)
L'ordonnée du point A d'abscisse 1 est \(\frac{5}{4}\)
Question
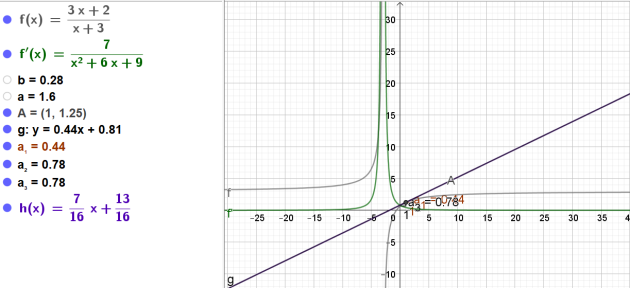
4.Déduire de la question précédente l'équation de la tangente
à la courbe représentative de la fonction \(f\) au point d'abscisse 1.
Solution
L'équation de la tangente \(T_A\) à la courbe représentative de la fonction \(f\)
au point d'abscisse 1 est de la forme
\(y=\frac{7}{16}x+b\)
or le point \(A(1;\frac{5}{4})\in T_A\)
\(\iff \frac{5}{4}=\frac{7}{16} \times 1+b\)
\(\iff \frac{5}{4}=\frac{7}{16}+b\)
\(\iff \frac{7}{16}+b=\frac{5}{4}\)
\(\iff b=\frac{5}{4}-\frac{7}{16}\)
\(\iff b=\frac{20}{16}-\frac{7}{16}\)
\(\iff b=\frac{13}{16}\)
L'équation de la tangente \(T_A\) à la courbe représentative de la fonction \(f\)
au point d'abscisse 1 est donc \(y=\frac{7}{16}x+\frac{13}{16}\)
