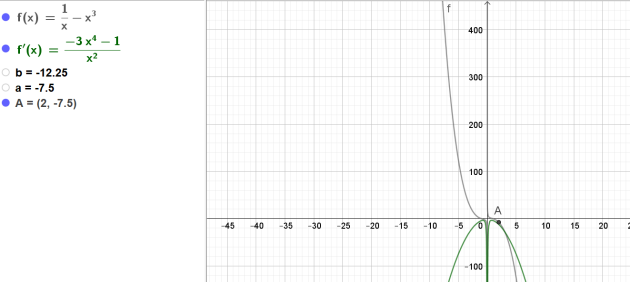
Exercice : 1/x-x^3
\(f\) est la fonction définie sur \(]0 ;+\infty[\) par \(f(x)=\frac{1}{x}-x^3\)
Question
Question
2.Quel est le coefficient directeur de la tangente à la courbe représentative
au point A d'abscisse 1 ?
Question
3.Quelle est l'ordonnée du point A ?
Question
4.Déduire de la question précédente l'équation de la tangente
à la courbe représentative de la fonction \(f\) au point d'abscisse 1.
Solution
L'équation de la tangente \(T_A\) à la courbe représentative de la fonction \(f\)
au point d'abscisse 1 est de la forme
\(y=-4x+b\)
or le point \(A(1;0)\in T_A\)
\(\iff 0=-4 \times 1+b\)
\(\iff 0=-4+b\)
\(\iff -4+b=0\)
\(\iff b=4\)
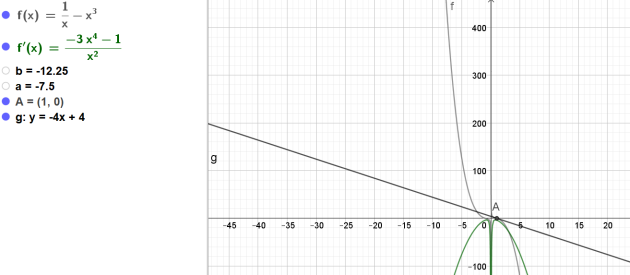
L'équation de la tangente \(T_A\) à la courbe représentative de la fonction \(f\)
au point d'abscisse 1 est donc \(y=-4x+4\)