Exercice : Etude Complète
\(g\) est définie sur [0 ;12] par la formule :
\(g(x)=-x^3+21x^2-120x+300\)
La fonction est représentée ci-dessous :
Question
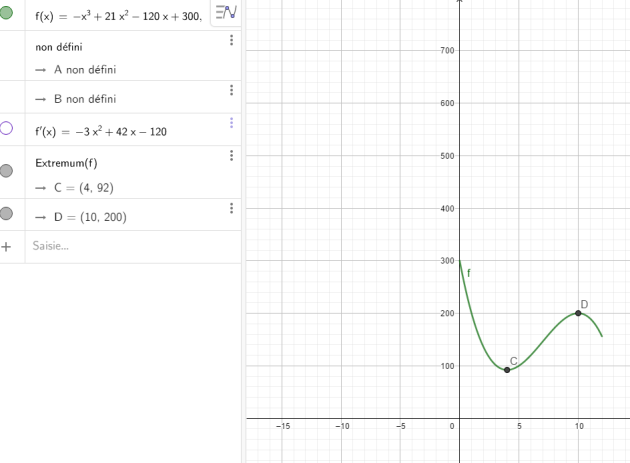
1.Compléter , à l'aide de sa représentation graphique et de l'expression de la fonction , le tableau de variations de \(g\)
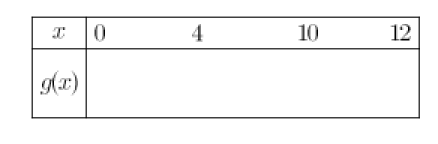
Solution
\(g(0)=-0^3+21\times 0^2-120 \times 0+300\)
\(\iff g(0)=300\)
\(g(4)=-4^3+21\times 4^2-120 \times 4+300\)
\(\iff g(4)=-64+21\times 16-480+300\)
\(\iff g(4)=-64+336-480+300\)
\(\iff g(4)=636-544=92\)
\(g(10)=-10^3+21\times 10^2-120 \times 10+300\)
\(\iff g(10)=-1000+21\times 100-1200+300\)
\(\iff g(10)=-1000+2100-1200+300=200\)
\(g(12)=-12^3+21\times 12^2-120 \times 12+300\)
\(\iff g(12)=-1728+3024-1440+300\)
\(\iff g(12)=3324-3168=156\)
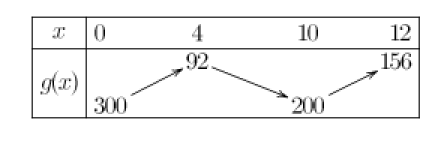
Question
2.a.Calculer la dérivée de g
Solution
\(g'(x)=-3x^2+21 \times 2x-120\)
\(\iff g'(x)=-3x^2+42x-120\)
Question
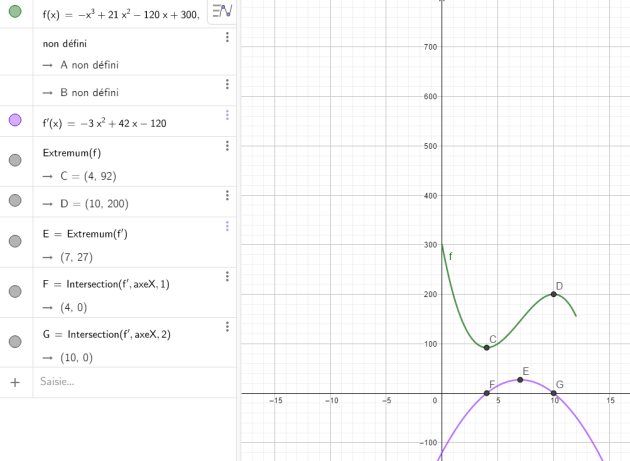
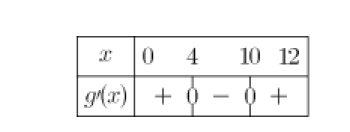
b. Déterminer le tableau de signes de \(g'\).
Solution
\(g'(x)=-3x^2+42x-120\) est une fonction polynôme du second degré.
\(\Delta=b^2-4ac\)
\(\iff \Delta=42^2-4\times(-3)\times (-120)\)
\(\iff \Delta=42^2-12 \times 120\)
\(\iff \Delta=1764-1440=324>0\) donc l'équation admet deux solutions.
\(\begin{cases}x_1=\frac{-b-\sqrt{\Delta}}{2a}\\x_2=\frac{-b+\sqrt{\Delta}}{2a}\end{cases}\)
\(\begin{cases}x_1=\frac{-42-\sqrt{324}}{2\times(-3)}\\x_2=\frac{-42+\sqrt{324}}{2\times(-3)}\end{cases}\)
\(\begin{cases}x_1=\frac{-42-18}{-6}\\x_2=\frac{-42+18}{-6}\end{cases}\)
\(\begin{cases}x_1=\frac{-60}{-6}\\x_2=\frac{-24}{-6}\end{cases}\)
\(\begin{cases}x_1=10\\x_2=4\end{cases}\)
Question
c.Comparer le tableaux de variations de la fonction \(g\) et le tableau de signes de la fonction \(g'\).
Quel lien semble-t-il y avoir entre signe de la fonction dérivée et variations de la fonction ?
Solution
\(\color{red}{Théorème : }\)
Soit une fonction f définie et dérivable sur un intervalle I.
- Si \(\color{magenta}{f'(x) \le 0}\), alors \(f\) est décroissante sur I.
- Si \(\color{magenta}{f'(x) \ge 0}\) , alors \(f\) est croissante sur I.