Exercice : Démonstration de formules du cours
Déterminer la fonction dérivée des fonctions suivantes :
Question
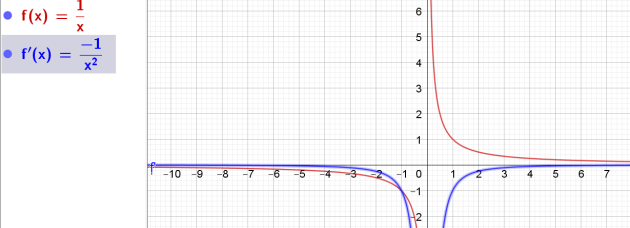
1.Soit la fonction \(f\) définie sur \(\mathbf{R}\)\{0} par \(f(x)=\frac{1}{x}\),
Solution
Pour \(h \ne 0\) :
\(\frac{f(a+h)-f(a)}{h}=\frac{\frac{1}{a+h}-\frac{1}{a}}{h}\)
\(=\frac{\frac{a-a-h}{a(a+h)}}{h}=\frac{-1}{a(a+h)}\)
Or :
\(lim_{h \to 0} \frac{f(a+h)-f(a)}{h}\)
\(= lim_{h \to 0} \frac{-1}{a(a+h)}\)
\(= \frac{-1}{a^2}\)
Pour tout nombre \(a\), on associe le nombre dérivé de la fonction f égal à \(\frac{-1}{a^2}\).
Ainsi, pour tout \(x\) de \(\mathbf{R}\)\{0}, on a : \(f'(x)=\frac{-1}{x^2}\).
Question
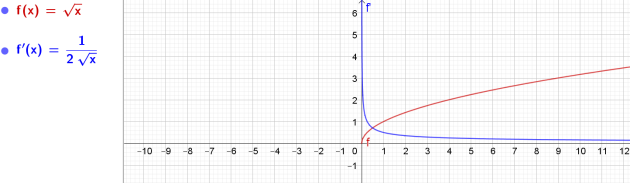
2.Soit la fonction \(f\) définie sur \(\mathbb{R}^+\) par \(f(x)=\sqrt{x}\)
Solution
Pour \(h \ne 0\) :
\(\frac{f(a+h)-f(a)}{h}\)
\(=\frac{\sqrt{a+h}-\sqrt{a}}{h}=\frac{\sqrt{a+h}-\sqrt{a}}{h}\)
\(=\frac{(\sqrt{a+h}+\sqrt{a})(\sqrt{a+h}-\sqrt{a})}{(\sqrt{a+h}+\sqrt{a})h}=\frac{(\sqrt{a+h})^2-(\sqrt{a})^2}{(\sqrt{a+h}+\sqrt{a})h}\)
\(=\frac{a+h-a}{(\sqrt{a+h}+\sqrt{a})h}\)
\(=\frac{h}{(\sqrt{a+h}+\sqrt{a})h}\)
\(=\frac{1}{(\sqrt{a+h}+\sqrt{a})}\)
Donc \(lim_{h\to 0} \frac{f(a+h)-f(a)}{h}=\frac{1}{2\sqrt{a}}\) a≠0
Pour tout nombre a≠0, on associe le nombre dérivé de la fonction \(f\) égal à \(\frac{1}{2\sqrt{a}}\).
Ainsi, pour tout \(x\) de \(\mathbb{R}_+^*\), on a : \(f'(x)=\frac{1}{2\sqrt{x}}\)