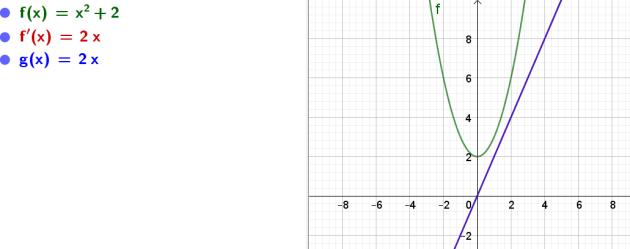
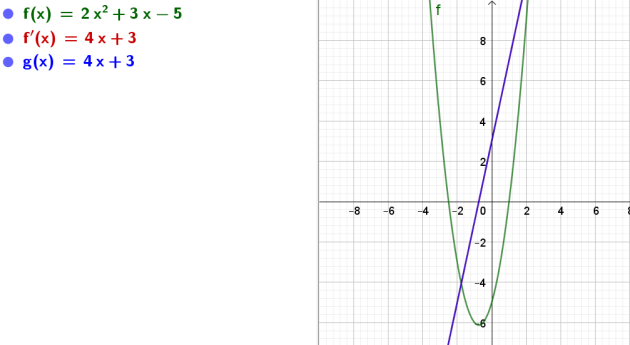
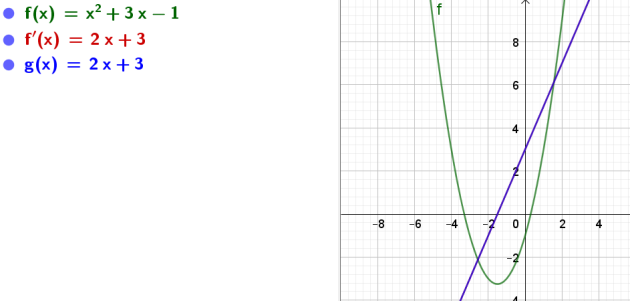
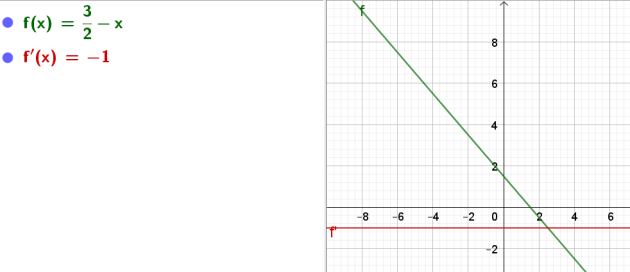
Exercice : Exercices d'applications du 2eme tableau 2

On donne la fonction \(f\) définie par l'expression \(f(x)\).

Déterminer l'expression \(f′(x)\) où \(f′\) désigne la fonction dérivée de \(f\)

ainsi que l'ensemble de définition des fonctions :

Question

\(a(x) = 2001\)

Indice

\(k \mapsto 0\)

Solution

\(a'(x)=0\) \(D_a=\mathbb{R}\) \(D_{a'}=\mathbb{R}\)

Question

\(b(x) = x^2 + 2\)

Indice

\(u+v \mapsto u'+v'\)

\(x^2 \mapsto 2x\)

\(k \mapsto 0\)

Solution

\(b'(x)=2x+0=2x\) \(D_b=\mathbb{R}\) \(D_{b'}=\mathbb{R}\)

Question

\(c(x) = 2x^2 + 3x − 5\)

Indice

\(ku \mapsto ku'\)

\(u+v \mapsto u'+v'\)

\(x \mapsto 1\)

\(x^2 \mapsto 2x\)

\(k \mapsto 0\)

Solution

\(c'(x)=4x+3\) \(D_b=\mathbb{R}\) \(D_{b'}=\mathbb{R}\)

Question

\(d(x) = x^2 + 3x − 1\)

Indice

\(ku \mapsto ku'\)

\(u+v \mapsto u'+v'\)

\(x^n \mapsto nx^{n-1}\)

\(k \mapsto 0\)

Solution

\(d'(x)=2x+3\) \(D_d=\mathbb{R}\) \(D_{d'}=\mathbb{R}\)

Question

\(e(x) = \frac{3}{2}-x\)

Indice

\(ku \mapsto ku'\)

\(k \mapsto 0\)

\(x \mapsto 1\)

Solution

\(e'(x)=0-1=-1\)

\(D_e=\mathbb{R}\) \(D_{e'}=\mathbb{R}\)\(\)\(\)

Question

\(f(x) = −2x^4 +\frac{5}{3} \times x^3\)

Indice

\(ku \mapsto ku'\)

\(u+v \mapsto u'+v'\)

\(k \mapsto 0\)

\(x^n \mapsto nx^{n-1}\)

Solution

\(f'(x) = −2 \times 4x^3 +\frac{5}{3} \times 3x^2\)

\(\iff f'(x) = −8x^3 +5x^2\)

\(D_f=\mathbb{R}\) \(D_{f'}=\mathbb{R}\)

Question

\(g(x)= 12x^{13} + 3x^{2}− 5x + \pi\)

Indice

\(k \mapsto 0\)

\(ku \mapsto ku'\)

\(u+v \mapsto u'+v'\)

\(uv \mapsto u'v+uv'\)

\(k \mapsto 0\)

\(x^n \mapsto nx^{n-1}\)

Solution

\(g'(x)= 12\times 13x^{12} + 3 \times 2x− 5\times 1+ 0\)

\(\iff g'(x)= 156x^{12} + 6x− 5\)

\(D_g=\mathbb{R}\) \(D_{g'}=\mathbb{R}\)

Question

\(h(x)=−5x^2 + 2x + \sqrt{2}\)

Indice

\(ku \mapsto ku'\)

\(u+v \mapsto u'+v'\)

\(x^n \mapsto nx^{n-1}\)

Solution

\(h'(x)=-5\times 2x +2 \times 1 +0\)

\(\iff h'(x)=-10x+2\)

\(D_h=\mathbb{R}\)\(D_{h'}=\mathbb{R}\)

Question

\(i(x)=−\frac{5x^3}{3}+ 3\)

Indice

\(k \mapsto 0\)

\(u+v \mapsto u'+v'\)

\(x^n \mapsto nx^{n-1}\)

\(ku \mapsto ku'\)

Solution

\(i'(x)=−\frac{5}{3} \times 3x^2 + 0\)

\(\iff i' (x)=-5x^2\)

donc \(D_i=\mathbb{R}\)\(D_{i'}=\mathbb{R}\)

Question

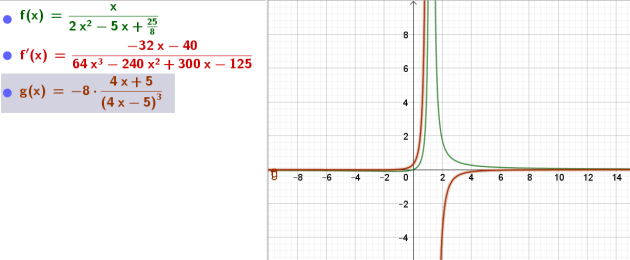
\(j(x)=\frac{x}{ 2x² - 5x + \frac{25}{8}}\)

Indice

\(\frac{u}{v} \mapsto \frac{u'v-uv'}{v^2}\)

\(k \mapsto 0\)

\(u+v \mapsto u'+v'\)

\(ku \mapsto ku'\)

\(x^n \mapsto nx^{n-1}\)

Solution

\(\begin{cases}u=x\\v=2x^2-5x+\frac{25}{8}\end{cases}\)

\(\iff \begin{cases}u'=1\\v'=4x-5\end{cases}\)

\(j'(x)=\frac{1(2x^2-5x+\frac{25}{8})-x(4x-5)}{(2x^2-5x+\frac{25}{8})^2}\)

\(\iff j'(x)=\frac{2x^2-5x+\frac{25}{8}-4x^2+5x}{(2x^2-5x+\frac{25}{8})^2}\)

\(\iff j'(x)=\frac{-2x^2+\frac{25}{8}}{(2x^2-5x+\frac{25}{8})^2}\)

\(2x^2-5x+\frac{25}{8}=0\) (2)

\(\Delta=b^2-4ac\)

\(\iff \Delta=(-5)^2-4\times 2 \times \frac{25}{8}\)

\(\iff \Delta=25-25=0\)

donc une unique solution à l'équation (2)

\(x_0=\frac{-b}{2a}=\frac{-(-5)}{2\times2}=\frac{5}{4}\)

\(\iff j'(x)=\frac{-2x^2+\frac{25}{8}}{(2(x-\frac{5}{4})^2)^2}\)

\(\iff j'(x)=\frac{-2x^2+\frac{25}{8}}{(\frac{2}{16}(4x-5)^2)^2}\)

\(\iff j'(x)=\frac{-2x^2+\frac{25}{8}}{(\frac{1}{8})^2(4x-5)^4}\)

\(\iff j'(x)=\frac{-2x^2+\frac{25}{8}}{\frac{1}{8^2}(4x-5)^4}\)

\(\iff j'(x)=\frac{-2x^2+\frac{25}{8}}{(4x-5)^4} \times \frac{8^2}{1}\)

\(\iff j'(x)=8\frac{-16x^2+25}{(4x-5)^4}\)

\(16x^2-25=(4x-5)(4x+5)\)

\(j'(x)=8\frac{-(4x-5)(4x+5)}{(4x-5)^4}\)

\(j'(x)=8\frac{-(4x+5)}{(4x-5)^3}\)

\(j'(x)=\frac{-8(4x+5)}{(4x-5)^3}\)

donc \(D_j=\mathbb{R}\backslash\{\frac{5}{4}\}\)\(D_{j'}=\mathbb{R}\backslash\{\frac{5}{4}\}\)

Question

\(k(x)=3(x − 4)\)

Indice

\(k \mapsto 0\)

\(u+v \mapsto u'+v'\)

\(ku \mapsto ku'\)

\(x \mapsto 1\)

Solution

\(k'(x)=3 \times 1=3\)

donc \(D_k=\mathbb{R}\)

\(D_{k'}=\mathbb{R}\)

Question

\(l(x)= −6(x^3− \pi x + 1)\)

Indice

\(k \mapsto 0\)

\(u+v \mapsto u'+v'\)

\(ku \mapsto ku'\)

\(x^n \mapsto nx^{n-1}\)

Solution

\(l'(x)= −6(3x^2− \pi)=-18x^2+6\pi\)

\(D_l=\mathbb{R}\)

\(D_{l'}=\mathbb{R}\)

Question

\(m(x)=−2(\frac{1}{3}x^2−\frac{2}{3}x − 1)\)

Indice

\(k \mapsto 0\)

\(u+v \mapsto u'+v'\)

\(ku \mapsto ku'\)

\(x^n \mapsto nx^{n-1}\)

Solution

\(m'(x)=−2(\frac{1}{3}\times 2x−\frac{2}{3} )=\frac{-4}{3}x+\frac{4}{3} )\)

\(D_m=\mathbb{R}\)

\(D_{m'}=\mathbb{R}\)

Question

\(o(x)=\frac{1}{2}(4x − 2x^3 + x^4 + 1)\)

Indice

\(k \mapsto 0\)

\(u+v \mapsto u'+v'\)

\(ku \mapsto ku'\)

\(x^n \mapsto nx^{n-1}\)

Solution

\(o'(x)=\frac{1}{2}(4 − 2\times 3x^2 + 4x^3)\)

\(\iff o'(x)=\frac{1}{2}(4x^3 − 6x^2+4)\)

\(\iff o'(x)=2x^3 − 3x^2+2\)

donc \(D_o=\mathbb{R}\)

\(D_{o'}=\mathbb{R}\)

Question

\(p(x)=3(\frac{x}{3} − 3)\)

Indice

\(k \mapsto 0\)

\(u+v \mapsto u'+v'\)

\(ku \mapsto ku'\)

\(x^n \mapsto nx^{n-1}\)

Solution

\(p'(x)=3(\frac{x}{3} − 3)\)

\(\iff p'(x)=3(\frac{1}{3})\)

\(\iff p'(x)=1\)

donc \(D_p=\mathbb{R}\)

\(D_{p'}=\mathbb{R}\)

Question

\(q(x)=−5(\sqrt{x} − 1)\)

Indice

\(k \mapsto 0\)

\(u+v \mapsto u'+v'\)

\(ku \mapsto ku'\)

\(\sqrt{x} \mapsto \frac{1}{2\sqrt{x}}\)

Solution

\(q'(x)=−5(\frac{1}{2\sqrt{x}})\)

\(\iff q'(x)=\frac{-5}{2\sqrt{x}}\)

donc \(D_q=\mathbb{R}_+\)

\(D_{q'}=\mathbb{R}_+^*\)

Question

\(r(x)=(1 + 3x)^2\)

Indice

\(k \mapsto 0\)

\(x \mapsto 1\)

\(u+v \mapsto u'+v'\)

\(u^n \mapsto nu^{n-1} \times u'\)

Solution

\(r'(x)=2(1 + 3x) \times 3\)

\(\iff r'(x)=6(1+3x)=18x+6\)

donc \(D_r=\mathbb{R}\)

\(D_{r'}=\mathbb{R}\)

Question

\(r(x)= (x − 3)^3\)

Indice

\(k \mapsto 0\)

\(x \mapsto 1\)

\(u+v \mapsto u'+v'\)

\(u^n \mapsto nu^{n-1} \times u'\)

Solution

\(r'(x)=3(x-3)^2 \times 1\)

\(\iff r'(x)=3(x-3)^2=3(x^2-6x+9)=3x^2-18x+27\)

donc \(D_r=\mathbb{R}\)

\(D_{r'}=\mathbb{R}\)

Question

\(s(x)= (2x − 4)^4\)

Indice

\(k \mapsto 0\)

\(ku \mapsto ku'\)

\(x \mapsto 1\)

\(u+v \mapsto u'+v'\)

\(u^n \mapsto nu^{n-1} \times u'\)

Solution

\(s'(x)=4(2x-4)^3 \times 2\)

\(\iff s'(x)=8(2x-4)^3=8(8x^3 -48x^2 -32x -64)\)

\(\iff s'(x)=64x^3 -384x^2+768x -512\)

car

\((2x-4)^3=(2x-4)^2\times (2x-4)=(4x^2-16x+16) \times (2x-4)\)

\(\iff (2x-4)^3=4x^2 \times 2x +4x^2 \times (-4) +(-16x) \times 2x + (-16x)\times (-4)+16 \times 2x +16 \times (-4)\)

\(\iff (2x-4)^3=8x^3 -16x^2 -32x^2 +64x+32x -64=8x^3 -48x^2 +96x -64\)

donc \(D_s=\mathbb{R}\)

\(D_{s'}=\mathbb{R}\)

Question

\(t(x)= (1 − 4x)^5\)

Indice

\(k \mapsto 0\)

\(ku \mapsto ku'\)

\(x \mapsto 1\)

\(u+v \mapsto u'+v'\)

\(u^n \mapsto nu^{n-1} \times u'\)

Solution

\(t'(x)=5(1 − 4x)^4 \times (-4)\)

\(\iff t'(x)=-20(1-4x)^4=-20(256x^4-256x^3+96x^2-16x+1)\)

\(\iff t'(x)=-5120x^4+5120x^3-11920x^2+32x-20\)

car

\((1-4x)^2=1-8x+16x^2\)

\((1-4x)^4=(1-8x+16x^2)(1-8x+16x^2)=1-8x+16x^2-8x+64x^2-128x^3+16x^2-128x^3+256x^4\)

\((1-4x)^4=256x^4-256x^3+96x^2-16x+1\)

donc \(D_t=\mathbb{R}\)

\(D_{t'}=\mathbb{R}\)

Question

\(u(x)= 5\sqrt{x}+ \frac{1}{2x}\)

Indice

\(ku \mapsto ku'\)

\(\sqrt{x} \mapsto \frac{1}{2\sqrt{x}}\)

\(u+v \mapsto u'+v'\)

\(\frac{1}{u}\mapsto \frac{-u'}{u^2}\)

Solution

\(u'(x)= 5\frac{1}{2\sqrt{x}}+ \frac{-2}{(2x)^2}\)

\(u'(x)= 5\frac{1}{2\sqrt{x}}+ \frac{-2}{4x^2}\)

\(u'(x)= 5\frac{2x\sqrt{x}}{4x^2}+ \frac{-2}{4x^2}\)

\(u'(x)= \frac{10x\sqrt{x}}{4x^2}+ \frac{-2}{4x^2}\)

\(u'(x)= \frac{10x\sqrt{x}-2}{4x^2}\)

\(u'(x)= \frac{5x\sqrt{x}-1}{2x^2}\)

\(u'(x)= \frac{5x^2-\sqrt{x}}{2x^2\sqrt{x}}\)

donc \(D_s=\mathbb{R}_+\)

\(D_{s'}=\mathbb{R}_+^*\)

Question

\(v(x)=\frac{3x-4}{2x+7}\)

Indice

\(ku \mapsto ku'\)

\(x \mapsto 1\)

\(u+v \mapsto u'+v'\)

\(\frac{u}{v}\mapsto \frac{u'v-uv}{v^2}\)

Solution

\(\begin{cases}u=3x-4\\v=2x+7\end{cases}\)

\(\iff \begin{cases}u'=3\\v'=2\end{cases}\)

\(v'(x)=\frac{3(2x+7)-(3x-4)\times 2}{(2x+7)^2}\)

\(\iff v'(x)=\frac{6x+21-6x+8}{(2x+7)^2}\)

\(\iff v'(x)=\frac{29}{(2x+7)^2}\)

\(2x+7=0\)

\(\iff 2x=-7\)

\(\iff x=-3,5\)

donc \(D_v=\mathbb{R}\backslash\{-3,5\}\)

\(D_{v'}=\mathbb{R}\backslash\{-3,5\}\)