III Détermination de l'équation de la tangente
Exemple : Exemple 1
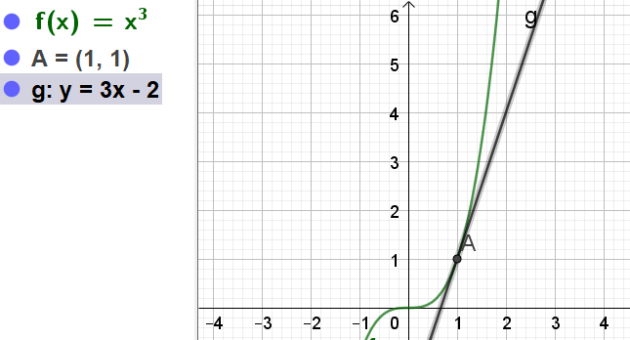
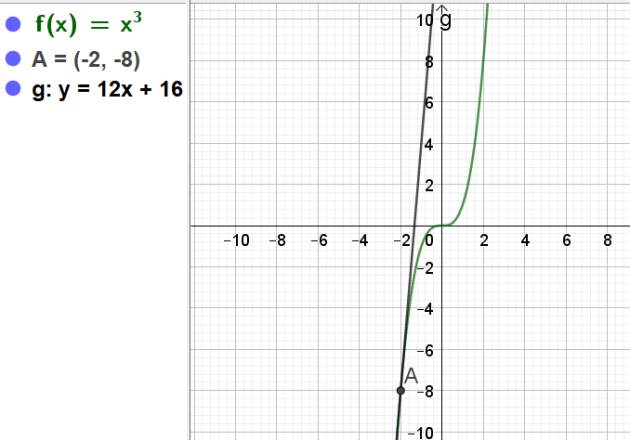
Soit \(f\) la fonction définie sur\( \mathbf{R}\) par \(f(x)=x^3\) et C sa courbe représentative.
A est le point d'abscisse 1 de la courbe C
a.Déterminer une équation de la tangente à C en A
Tracer la courbe C et la tangente T
Complément :
\(T(x)=f'(a)(x-a)+f(a)\)
\(f(x)=x^3\)
\(f'(x)=3x^2\)
\(\iff T(x)=f'(1)(x-1)+f(1)\)
\(f'(1)=3\times 1^2=3\)
\(f(1)=1^3=1\)
\(T(x)=3(x-1)+1\)
\(\iff T(x)=3x-3+1=3x-2\)
Exemple :
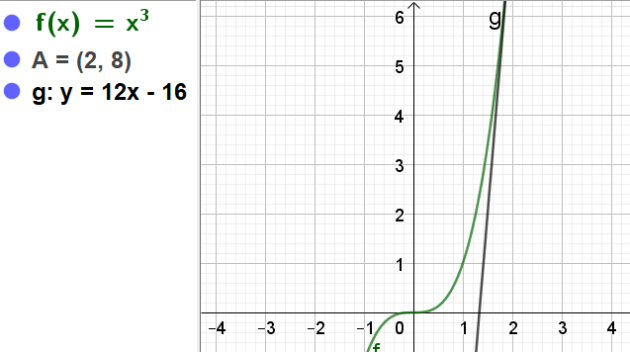
b.Existe-t-il une tangente à C de coefficient directeur 12 ?
Si oui, déterminer les coordonnées des points de contact éventuels.
Complément :
Une tangente à C de coefficient directeur 12 signifie
\(f'(x)=3x^2=12\)
\(\iff x^2=4\)
\(\iff x=2\) ou \(x=-2\)
\(\color{magenta}{\text{L'équation au point d'abscisse 2 est :}}\)
\(T(x)=f'(2)(x-2)+f(2)\)
\(f'(2)=3\times 2^2=12\)
\(f(2)=2^3=8\)
\(T(x)=12(x-2)+8\)
\(\iff T(x)=12x-24+8=12x-16\)
\(\color{magenta}{\text{L'équation au point d'abscisse -2 est :}}\)
\(T(x)=f'(-2)(x-(-2))+f(-2)\)
\(f'(-2)=3\times (-2)^2=12\)
\(f(2)=(-2)^3=-8\)
\(T(x)=12(x+2)-8\)
\(\iff T(x)=12x+24-8=12x+16\)
Exemple : Exemple 2
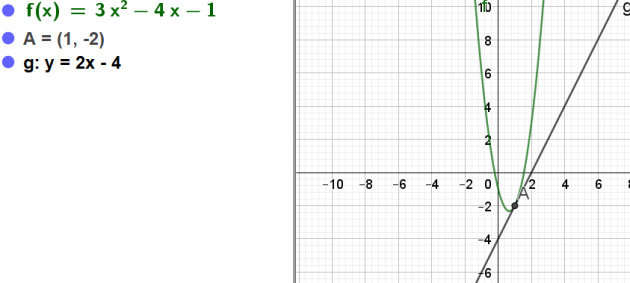
On donne la fonction \(f\) définie sur \(\mathbf{R}\) par \(f(x)=3x^2-4x-1\)
Déterminer une équation de la tangente à la courbe en \(x=1\)
Complément :
\(T(x)=f'(1)(x-1)+f(1)\)
\(f(1)=3\times 1^2-4 \times 1-1=3-4-1=-2\)
\(f'(x)=3\times 2x-4 \times 1\)
\(\iff f'(x)=6x-4\)
\(f'(1)=6\times 1-4=6-4=2\)
\(T(x)=2(x-1)-2\)
\(\iff T(x)=2x-2-2=2x-4\)
Exemple : Exemple 3
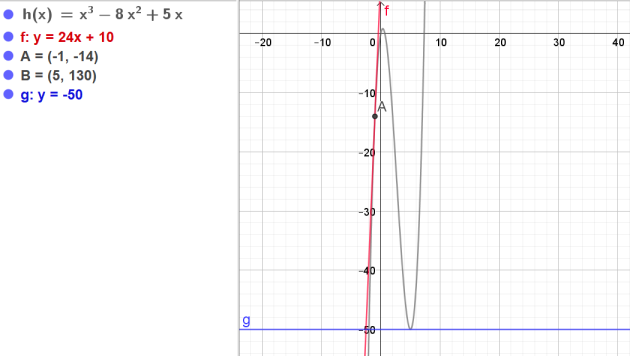
Soit \(f\) la fonction définie sur \(\mathbb{R}\) par \(f(x)=x^3-8x^2+5x\)
et \(C_f \)sa représentation graphique dans un repère.
a.Déterminer un équation de la tangente \((T_1)\) à la courbe \(C_f\) au point A d'abscisse 5.
b.Déterminer un équation de la tangente \((T_2)\) à la courbe \(C_f\) au point B d'abscisse -1.
c.Dans un repère, tracer la courbe \(C_f\), \((T_1)\) et \((T_2)\)
Complément :
a.\(T(x)=f'(5)(x-5)+f(5)\)
\(f(5)=5^3-8\times 5^2+5 \times 5\)
\(\iff f(5)=125-200+25\)
\(\iff f(5)=-50\)
\(f'(x)=3\times x^2-8 \times 2x+5\)
\(f'(x)=3x^2-16x+5\)
\(f'(5)=3\times 5^2-16\times 5+5\)
\(\iff f'(5)=3\times 25-80+5\)
\(\iff f'(5)=0\)
\(T(x)=0(x-5)-50=-50\)
b.\(T(x)=f'(-1)(x-(-1))+f(-1)\)
\(f(-1)=(-1)^3-8\times (-1)^2+5 \times (-1)\)
\(\iff f(-1)=-1-8\times 1-5\)
\(\iff f(-1)=-1-8-5\)
\(\iff f(-1)=-14\)
\(f'(x)=3x^2-16x+5\)
\(f'(-1)=3\times (-1)^2-16\times (-1)+5\)
\(\iff f'(-1)=3\times 1+16+5\)
\(\iff f'(-1)=24\)
\(T(x)=24(x-(-1))-14=24(x+1)-14\)
\(\iff T(x)=24x+24-14\)
\(\iff T(x)=24x+10\)
Exemple : Exemple 4
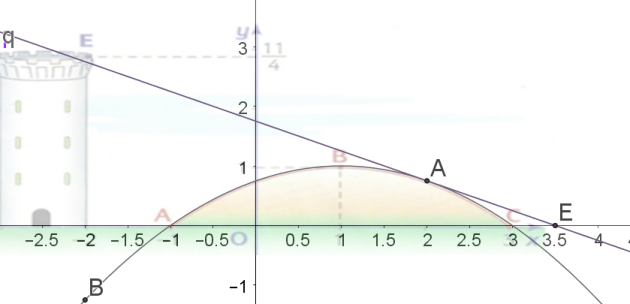
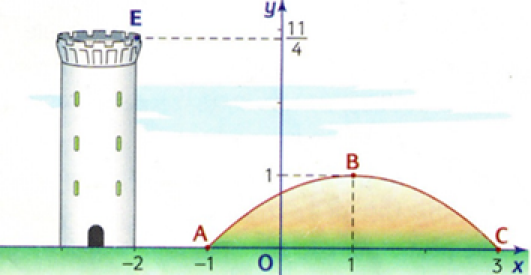
Sur la figure ci-dessous , l'arc de parabole ABC représente une colline, le sol est symbolisé par l'axe des abscisses.
Un observateur est placé en E de coordonnée \((-2 ;\frac{11}{4})\) dans le repère choisi.
Le but de cet exercice est de déterminer les points de la colline et ceux du sol (au-delà de la colline) qui ne sont pas visibles du point d'observation E.
Complément :
Equation de l'arc de parabole ABC :
\(f(x)=a(x-\alpha)^2+\beta\)
\(\iff f(x)=a(x-1)^2+1\)
or la parabole passe par le point A
donc
\(f(-1)=a(-1-1)^2+1\)
\(\iff f(-1)=a(-2)^2+1=0\)
\(\iff a(-2)^2+1=0\)
\(\iff 4a+1=0\)
\(\iff 4a=-1\)
\(\iff a=\frac{-1}{4}\)
ou la parabole passe par le point B
donc \(f(3)=a(3-1)^2+1=0\)
\(\iff a\times 2^2+1=0\)
\(\iff a\times 4+1=0\)
\(\iff 4a+1=0\)
\(\iff 4a=-1\)
\(\iff a=\frac{-1}{4}\)
donc l'équation de l'arc de parabole ABC est :
\(f(x)=\frac{-1}{4}(x-1)^2+1\)
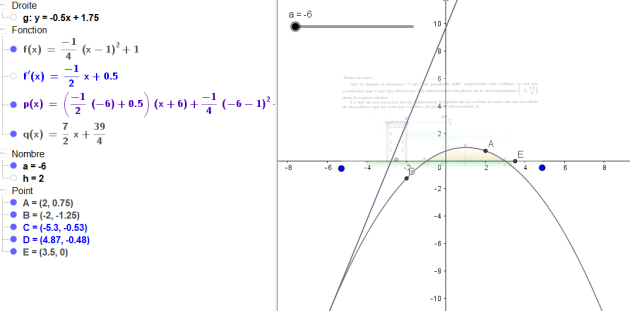
Déterminons l'équation de la tangente à l'arc de parabole ABC au point d'abscisse a :
\(y=f'(a)(x-a)+f(a)\)
\(f(x)=\frac{-1}{4}(x-1)^2+1\)
\(\iff f'(x)=\frac{-1}{4}\times 2\times (x-1)\)
\(\iff f'(x)=\frac{-1}{2}(x-1)\)
\(f'(a)=\frac{-1}{2}(a-1)\)
\(f(a)=\frac{-1}{4}(a-1)^2+1\)
\(y=\frac{-1}{2}(a-1)(x-a)+(\frac{-1}{4}(a-1)^2+1)\)
\(\iff y=\frac{-1}{2}(a-1)x+\frac{1}{2}(a-1)a-\frac{1}{4}(a^2-2a+1)+1\)
\(\iff y=\frac{-1}{2}(a-1)x+\frac{1}{2}(a-1)a-\frac{1}{4}(a^2-2a+1)+1\)
\(\iff y=\frac{-1}{2}(a-1)x+\frac{1}{2}(a-1)a-\frac{1}{4}a^2+\frac{1}{2}a-\frac{1}{4}+1\)
\(\iff y=\frac{-1}{2}(a-1)x+\frac{1}{2}a^2-\frac{1}{2}a-\frac{1}{4}a^2+\frac{1}{2}a-\frac{1}{4}+1\)
\(\iff y=\frac{-1}{2}(a-1)x+\frac{1}{4}a^2+\frac{3}{4}\)
\(E(-2 ;\frac{11}{4})\)
\(\iff \frac{11}{4}=\frac{-1}{2}(a-1)\times (-2)+\frac{1}{4}a^2+\frac{3}{4}\)
\(\iff \frac{11}{4}=a-1+\frac{1}{4}a^2+\frac{3}{4}\)
\(\iff \frac{11}{4}=\frac{1}{4}a^2+a-\frac{1}{4}\)
\(\iff 0=\frac{1}{4}a^2+a-\frac{12}{4}\)
\(\iff \frac{1}{4}a^2+a-\frac{12}{4}=0\)
\(\iff \frac{1}{4}a^2+a-3=0\)
\(\Delta=b^2-4ac\)
\(\iff \Delta=1^2-4(\frac{1}{4})(-3)\)
\(\iff \Delta=1+3=4>0\) donc l'équation a deux solutions.
\(\begin{cases}x_1=\frac{-b-\sqrt{\Delta}}{2a}\\x_2=\frac{-b+\sqrt{\Delta}}{2a}\end{cases}\)
\(\iff \begin{cases}x_1=\frac{-1-\sqrt{4}}{2\times \frac{1}{4}}\\x_2=\frac{-1+\sqrt{4}}{2 \times \frac{1}{4}}\end{cases}\)
\(\iff \begin{cases}x_1=\frac{-1-2}{\frac{1}{2}}\\x_2=\frac{-1+2}{\frac{1}{2}}\end{cases}\)
\(\iff \begin{cases}x_1=\frac{-3}{\frac{1}{2}}\\x_2=\frac{1}{\frac{1}{2}}\end{cases}\)
\(\iff \begin{cases}x_1=-3 \times 2\\x_2=1 \times 2\end{cases}\)
\(\iff \begin{cases}x_1=-6\\x_2=2\end{cases}\)
Il s'agit donc de chercher l'abscisse du point d'intersection entre la tangente au point d'abscisse 2 et de l'axe des abscisses.
\(y=f'(2)(x-2)+f(2)\)
\(f'(2)=\frac{-1}{2}(2-1)=\frac{-1}{2}(2-1)=\frac{-1}{2}\)
\(f(2)=\frac{-1}{4}(2-1)^2+1=\frac{-1}{4}+1=\frac{-1}{4}+\frac{4}{4}=\frac{3}{4}\)
\(y=\frac{-1}{2}(x-2)+\frac{3}{4}\)
\(\iff y=\frac{-1}{2}x+1+\frac{3}{4}\)
\(\iff y=\frac{-1}{2}x+\frac{7}{4}\)
\(y=\frac{-1}{2}x+\frac{7}{4}=0\)
\(\iff \frac{-1}{2}x=-\frac{7}{4}\)
\(\iff \frac{1}{2}x=\frac{7}{4}\)
\(\iff x=\frac{7}{4} \times 2=\frac{7}{2}=3,5\)
Les points qui seront cachés de la tourelle seront donc les points donc l'abscisse est comprise entre 3 et 3,5.
Exemple :
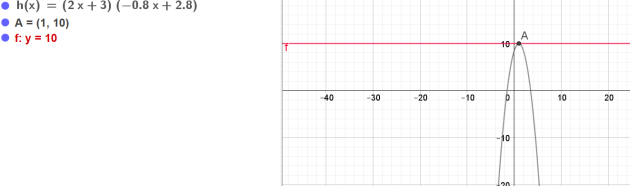
On considère une fonction \(v\), sa dérivée \(v'\) et la fonction \(h\) définie par \(h (x) = (2x + 3) v (x) .\)
1. Exprimer la dérivée \(h'(x)\).
2. On suppose que \(v(x)\) est une fonction affine.
Déterminer cette fonction de telle sorte que \(h (1) = 10\) et \(h' (1) = 0\).
Complément :
1.\(h (x) = (2x + 3) v (x)\)
\(h'(x) = 2\times v(x)+(2x + 3)\times v'(x)\)
2.\(v\) est une fonction affine donc
\(v(x)=ax+b\)
\(v'(x)=a\)
\(h'(x) = 2\times (ax+b)+(2x + 3)\times a\)
\(\iff h'(x) = 2ax+2b+2ax + 3a\)
\(\iff h'(x) = 4ax+ 2b + 3a\)
\(h (x) = (2x + 3)(ax+b)\)
\(h(1)= (2\times 1+ 3)(a \times 1+b)=10\)
\(\iff h(1)= 5(a+b)=10\)
\(h'(1)= 4a \times 1+ 2b + 3a=7a+2b=0\)
\(\begin{cases}a+b=2\\7a+2b=0\end{cases}\)
\(\begin{cases}7a+7b=14\\7a+2b=0\end{cases}\)
\(5b=14\)
\(\iff b=\frac{14}{5}=2,8\)
\(a+b=2\)
\(\iff a+2,8=2\)
\(\iff a=2-2,8=-0,8\)
donc \(v(x)=-0,8x+2,8\)
Exercices sur les suites
Exemple :
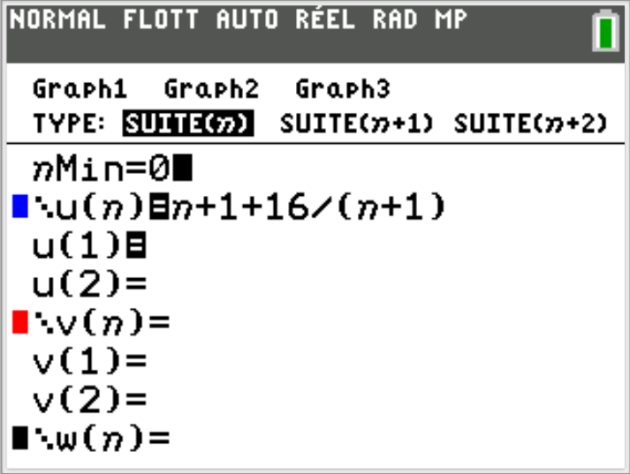
On considère la fonction \(f\) définie sur l'intervalle [0 ; +∞[ par :
\(f(x)= x + 1 +\frac{16}{x + 1}\)
et on définit la suite \(U\) par : \(U_n = f(n)\) ; ∀n ∈N.
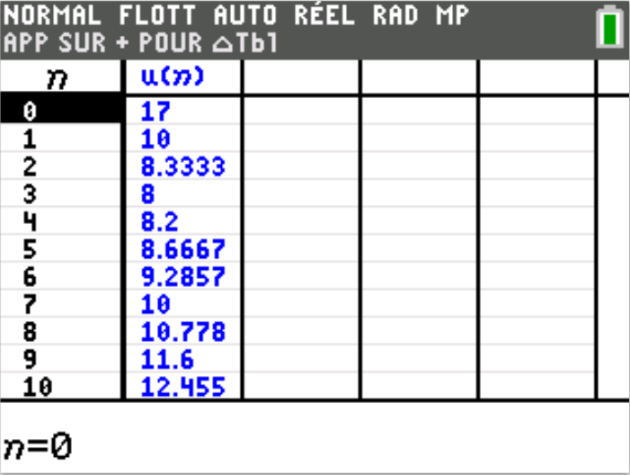
1. Obtenir à l'aide de la calculatrice une table des termes successifs de la suite \(U_n\).
2. Conjecturer le sens de variation de cette suite.
3. Prouver la conjecture en étudiant les variations de la fonction \(f.\)
Exemple :
\(f'(n)= 1 -\frac{16}{(n + 1)^2}\)
\(f'(n) \ge 0\)
\(\iff 1 -\frac{16}{(n + 1)^2} \ge 0\)
\(\iff -\frac{16}{(n + 1)^2} \ge -1\)
\(\iff -16 \ge -(n + 1)^2\)
\(\iff 16 \le (n+ 1)^2\)
\(\iff 4 \le n + 1 \)ou \(n+1 \le -4\)
\(\iff 3 \le n \)ou \(n \le -5\)
or \(n \in \mathbb{N}\) donc \(n \ge 0\)
\(f(0)= 0 + 1 +\frac{16}{0 + 1}\)
\(\iff f(0)= 1 +\frac{16}{1}\)
\(\iff f(0)= 17\)
\(f(3)= 3 + 1 +\frac{16}{3+ 1}\)
\(\iff f(3)= 4 +\frac{16}{4}\)
\(\iff f(0)= 4+4=8\)
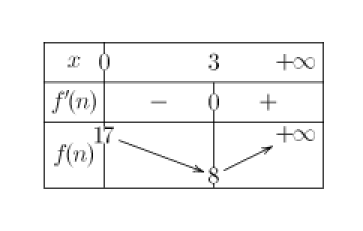
On en déduit que la conjecture est bien correcte.
La suite \((U_n)\) est décroissante jusqu'à l'indice 3 puis est croissante à partir de l'indice 3.