Exercice : DM Noël 2020
Donner les fonctions dérivées ainsi que les ensembles de définition de chacune des fonctions suivantes :
Question
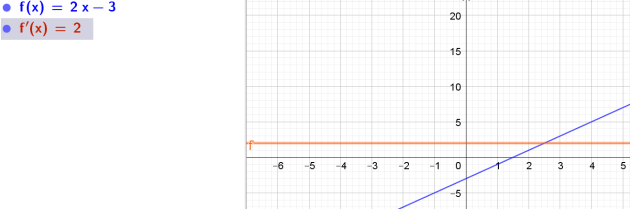
1.\(f(x)= 2x – 3\)
Solution
\(f'(x)= 2 \times 1 -0 =2\)
\(D_f=\mathbb{R}\)
\(D_{f'}=\mathbb{R}\)
Question
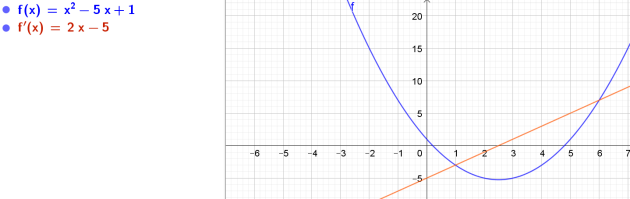
\(2. g (x)=x²-5x+1\)
Solution
\(g'(x)=2x-5\times 1+0=2x-5\)
\(D_g=\mathbb{R}\)
\(D_{g'}=\mathbb{R}\)
Question
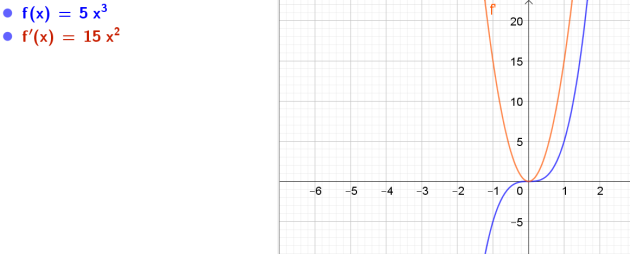
\(3. h(t)=5t^3\)
Solution
\(h'(t)=5 \times 3t^2=15t^2\)
\(D_h=\mathbb{R}\)
\(D_{h'}=\mathbb{R}\)
Question
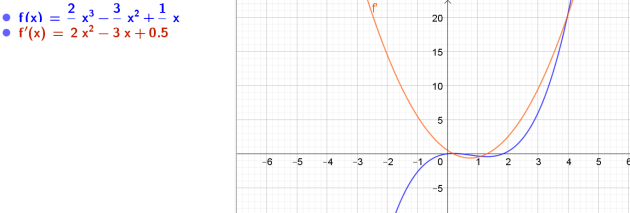
\(4. i(x)=\frac{2}{3} x^3-\frac{3}{2}x^2+\frac{1}{2}x\)
Solution
\(i'(x)=\frac{2}{3} \times 3x^2-\frac{3}{2} \times 2x+\frac{1}{2} \times 1\)
\(\iff i'(x)=2x^2-3x+\frac{1}{2}\)
\(D_i=\mathbb{R}\)
\(D_{i'}=\mathbb{R}\)
Question
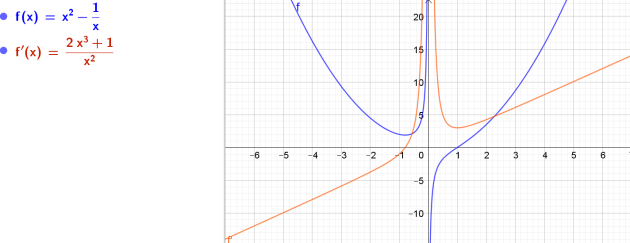
\(5. j(t)= t² - \frac{1}{t}\)
Solution
\(j'(t)=2t-\frac{-1}{t^2}\)
\(\iff j'(t)=2t+\frac{1}{t^2}\)
\(D_j=\mathbb{R}\backslash \{0\}\)
\(D_{j'}=\mathbb{R}\backslash \{0\}\)
Question
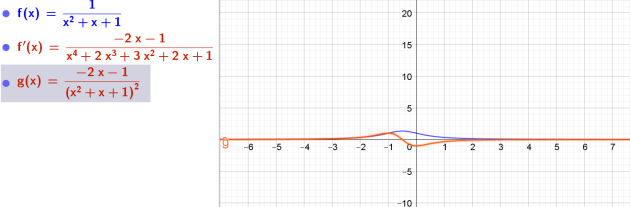
\(6. k(x)=\frac{1}{x^2+x+1}\)
Solution
\(k'(x)=\frac{-(2x+1)}{(x^2+x+1)^2}\)
\(\iff k'(x)=\frac{-2x-1}{(x^2+x+1)^2}\)
\(x^2+x+1=0\)
\(\Delta=b^2-4ac=1^2-4\times 1 \times 1=1-4=-3\)
donc l'équation (1) n'a pas de solution.
\(D_k=\mathbb{R}\)
\(D_{k'}=\mathbb{R}\)
Question
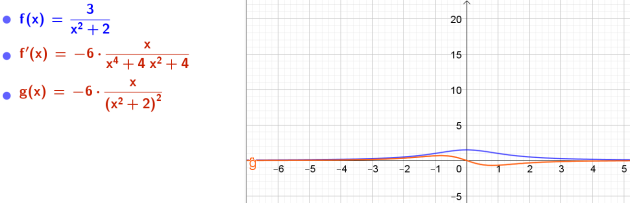
7.\( l(x)= \frac{3}{x^2+2}\)
Solution
\(l'(x)=3\times \frac{-2x}{(x^2+2)^2}\)
\(\iff l'(x)=\frac{-6x}{(x^2+2)^2}\)
\(x^2+2=0 \)(1)
\(\Delta=b^2-4ac=0^2-4\times 1 \times 2=-8\)
donc l'équation (1) n'a pas de solution.
\(D_l=\mathbb{R}\)
\(D_{l'}=\mathbb{R}\)
Question
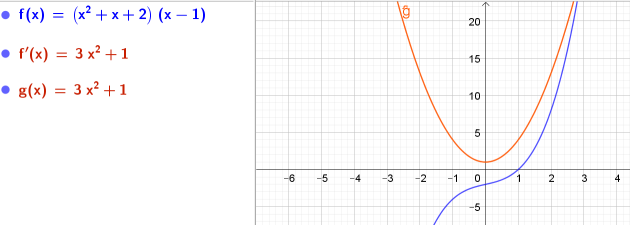
8. \(m(x)= (x²+x+2)(x-1)\)
Solution
\(\begin{cases}u=x^2+x+2\\v=x-1\end{cases}\)
\(\begin{cases}u'=2x+1\\v=1\end{cases}\)
\(m'(x)=(2x+1)(x-1)+(x^2+x+2)\times 1\)
\(\iff m'(x)=2x \times x+2x \times (-1)+1\times x+1\times (-1)+x^2+x+2\)
\(\iff m'(x)=2x^2-2x+x-1+x^2+x+2=3x^2+1\)
\(D_m=\mathbb{R}\)
\(D_{m'}=\mathbb{R}\)
Question
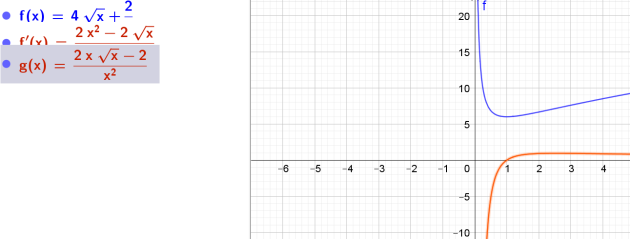
\(9. n(x) = 4 \sqrt{x} + \frac{2}{x}\)
Solution
\(n'(x)=4\times \frac{1}{2\sqrt{x}}+2\times \frac{-1}{x^2}\)
\(n'(x)=\frac{2}{\sqrt{x}}-\frac{2}{x^2}\)
\(D_n=]0;+\infty[\)
\(D_{n'}=]0;+\infty[\)
Question
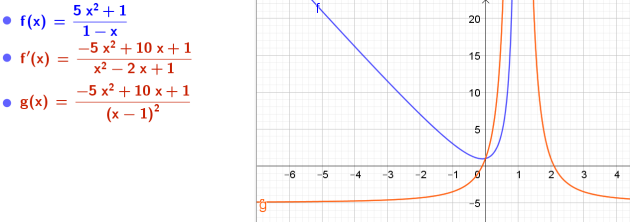
\(10. o(x) =\frac{5x² + 1}{1-x}\)
Solution
\(\begin{cases}u=5x^2+1\\v=1-x\end{cases}\)
\(\begin{cases}u'=5\times 2x\\v'=0-1\end{cases}\)
\(\begin{cases}u'=10x\\v'=-1\end{cases}\)
\(o'(x)= \frac{10x(1-x)-(5x^2+1)(-1)}{(1-x)^2}\)
\(\iff o'(x)=\frac{10x-10x^2-(-5x^2-1)}{(1-x)^2}\)
\(\iff o'(x)=\frac{10x-10x^2+5x^2+1}{(1-x)^2}\)
\(\iff o'(x)=\frac{-5x^2+10x+1}{(1-x)^2}\)
\(D_o=\mathbb{R}\backslash\{1\}\)
\(D_ {o'}=\mathbb{R}\backslash\{1\}\)
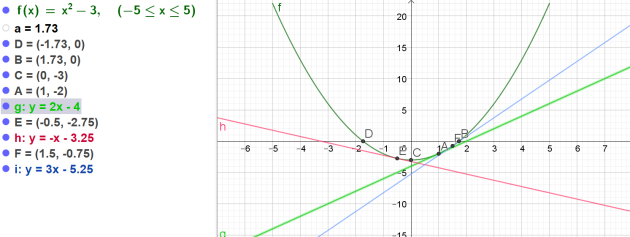
Soit \(f\) la fonction définie sur \(\mathbb{R}\) par \(f(x)=x^2-3\)
Question
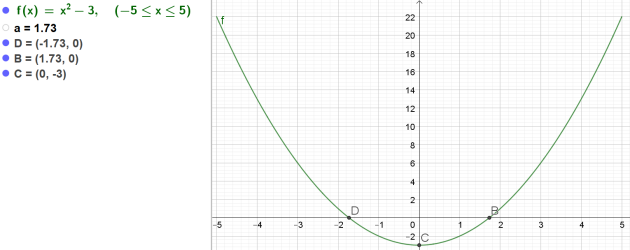
1.Tracer la représentation graphique \(\mathcal{C}\) de la fonction \(f\) sur [-5;5](utiliser une feuille de papier millimétré).
Pour ce faire, on déterminera en particulier :
- \(\alpha\),\(\beta\)
-les solutions de l'équation \(f(x)=0\)
Solution
\(\color{magenta}{\text{1ère méthode :}}\)
\(x^2-3=1(x-0)^2+(-3)\)
donc \(\alpha=0 \beta=-3 a=1\)
\(\color{magenta}{\text{2ème méthode :}}\)
\(\alpha=\frac{-b}{2a}=\frac{0}{2\times 1}=0\)
\(\beta=4 \times 0^2-3=-3\)
\(\Delta=b^2-4ac=0-4\times 1 \times (-3)=12>0\)
donc l'équation admet deux solutions :
\(\begin{cases}x_1=\frac{-b-\sqrt{\Delta}}{2a}\\x_2=\frac{-b+\sqrt{\Delta}}{2a}\end{cases}\)
\(\iff \begin{cases}x_1=\frac{-0-\sqrt{12}}{2\times 1}\\x_2=\frac{-0+\sqrt{12}}{2 \times 1}\end{cases}\)
\(\iff \begin{cases}x_1=\frac{-\sqrt{12}}{2}\\x_2=\frac{\sqrt{12}}{2}\end{cases}\)
\(\iff \begin{cases}x_1=\frac{-\sqrt{4\times 3}}{2}\\x_2=\frac{\sqrt{4\times 3}}{2}\end{cases}\)
\(\iff \begin{cases}x_1=\frac{-2\sqrt{3}}{2}\\x_2=\frac{2\sqrt{3}}{2}\end{cases}\)
\(\iff \begin{cases}x_1=-\sqrt{3}\\x_2=\sqrt{3}\end{cases}\)
or \(\sqrt{3}\simeq1,7\)
Question
2.Calculer la dérivée \(f'\) de \(f\)
Solution
\(f'(x)=2x-0=2x\)
Question
3.Soit A le point de \(\mathcal{C}\) d'abscisse 1.
a.Calculer le coefficient directeur de la tangente \((T_A)\)à \(\mathcal{C}\) en A.
Solution
Le coefficient directeur de la tangente \((T_A)\)à \(\mathcal{C}\) en A correspond au nombre dérivé au point d'abscisse
\(f'(1)=2 \times 1=2\)
Donc le coefficient directeur de la tangente \((T_A)\)à \(\mathcal{C}\) en A vaut 2
Question
b. La tangente (\(T_A\)) a une équation de la forme \(y=mx+p\)
En remplaçant par les coordonnées du point A déterminer l'ordonnée à l'origine \(p\) dans l'équation.
Solution
D'après la question 3.a.,
l'équation de la tangente \((T_A)\) au point A est de la forme :
\(y=2x+p\)
L'ordonnée du point A est \(y_A=f(1)=1^2-3=1-3=-2\)
Comme \(A \in (T_A)\):
\(-2=2\times 1+p\)
\(\iff -2=2+p\)
\(\iff 2+p=-2\)
\(\iff p=-2-2=-4\)
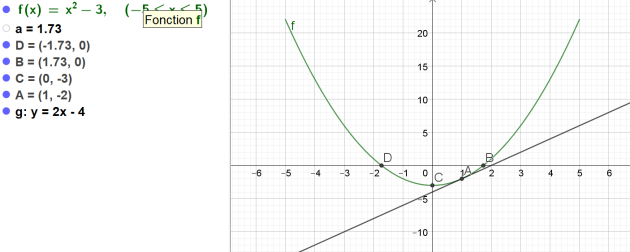
L'équation de la tangente \((T_A)\) est donc \(y=2x-4\)
Question
c.Tracer la tangente \((T_A)\) sur le graphique précédent.
Question
4. Même question qu'au 3., avec le point E de \(\mathcal{C}\) d'abscisse \(\frac{-1}{2}\)
puis avec le point F d'abscisse \(\frac{3}{2}\)
Solution
\(\color{red}{\text{Déterminons l'équation de la tangente au point E d'abscisse } \frac{-1}{2}}\)
\(f'(\frac{-1}{2})=2\times (\frac{-1}{2})=-1\)
l'équation de la tangente \((T_E)\) au point E est de la forme :
\(y=-1x+p\)
L'ordonnée du point E est
\(y_E=f(\frac{-1}{2})=(\frac{-1}{2})^2-3=\frac{1}{4}-3=\frac{1}{4}-\frac{12}{4}\)
\(\iff y_E=-\frac{11}{4}\)
Comme \(E \in (T_E)\):
\(-\frac{11}{4}=-1\times \frac{-1}{2}+p\)
\(\iff -\frac{11}{4}=\frac{1}{2}+p\)
\(\iff \frac{1}{2}+p=-\frac{11}{4}\)
\(\iff p=-\frac{11}{4}-\frac{1}{2}=-\frac{11}{4}-\frac{2}{4}\)
\(\iff p=-\frac{13}{4}=-3,25\)
L'équation de la tangente \((T_E)\) est donc \(y=-x-3,25\)
\(\color{red}{\text{Déterminons l'équation de la tangente au point F d'abscisse } \frac{3}{2}}\)
\(f'(\frac{3}{2})=2\times (\frac{3}{2})=3\)
l'équation de la tangente \((T_F)\) au point F est de la forme :
\(y=3x+p\)
L'ordonnée du point F est
\(y_F=f(\frac{3}{2})=(\frac{3}{2})^2-3=\frac{9}{4}-3=\frac{9}{4}-\frac{12}{4}\)
\(\iff y_F=-\frac{3}{4}\)
Comme \(F \in (T_F)\):
\(--\frac{3}{4}=3\times \frac{3}{2}+p\)
\(\iff -\frac{3}{4}=\frac{9}{2}+p\)
\(\iff \frac{9}{2}+p=-\frac{3}{4}\)
\(\iff p=-\frac{3}{4}-\frac{9}{2}=-\frac{3}{4}-\frac{18}{4}\)
\(\iff p=-\frac{21}{4}=-5,25\)
L'équation de la tangente \((T_F)\) est donc \(y=3x-5,25\)
Soit \(f\) la fonction définie sur \(\mathbb{R}\) dont le graphe est donné ci-dessous :
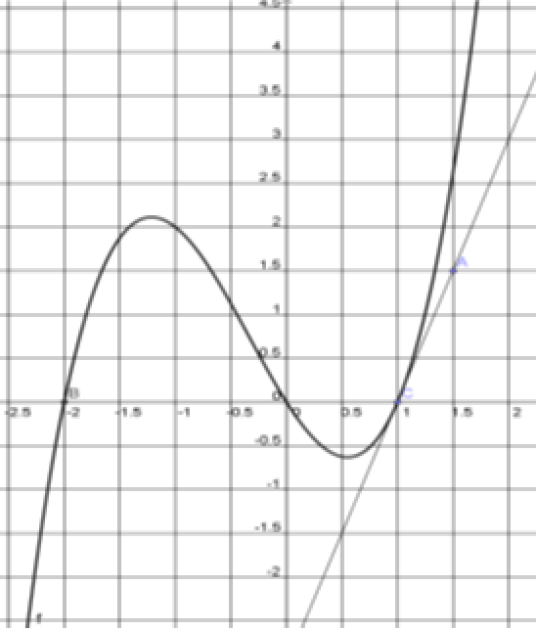
1.Par lecture graphique, déterminer :
Question
a. \(f(-1)\)
Solution
\(f(-1)=2\)
L'image de -1 est 2
Question
b.\(f'(1)\)
Solution
\(f'(1)=3\)
Le nombre dérivé de la fonction \(f\) au point d'abscisse 1
correspond au coefficient directeur de la tangente et vaut 3
Résoudre :
Question
a. \(f(x)=0\)
Solution
\(f(x)=0 \iff x_1=-2\) ; \(x_2=0\) et \(x_3=1\)
En effet la courbe de la fonction \(f\) coupe l'axe des abscisses en trois points d'abscisses \(x_1=-2\) ; \(x_2=0\) et \(x_3=1\)
Question
b. \(f'(x) > 0\)
(on donnera le résultat sous forme d'intervalles avec des valeurs approchées )
Solution
\(f'(x) > 0 pour x \in ]-\infty ;-1,25[\cup]0,6 ;+\infty[\)
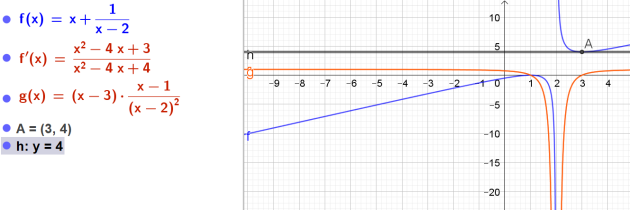
\(f\) est la fonction définie sur [3 ; +∞ [ par \(f(x)=x+\frac{1}{x-2}\)
Question
1. Déterminer sa fonction dérivée \(f'(x)\)
Solution
\(f'(x)=1+\frac{-1}{(x-2)^2}\)
\(\iff f'(x)=\frac{(x-2)^2}{(x-2)^2}+\frac{-1}{(x-2)^2}\)
\(\iff f'(x)=\frac{(x-2)^2-1}{(x-2)^2}\)
\(\iff f'(x)=\frac{(x-2)^2-1^2}{(x-2)^2}\)
\(\iff f'(x)=\frac{(x-2-1)(x-2+1)}{(x-2)^2}\)
\(\iff f'(x)=\frac{(x-3)(x-1)}{(x-2)^2}\)
Question
2. Déterminer une équation de la tangente à la courbe représentant la fonction \(f\) au point d'abscisse 3.
Solution
\(f'(3)=\frac{(3-3)(3-1)}{(3-2)^2}\)
\(\iff f'(3)=\frac{0 \times 2}{1}\)
\(\iff f'(3)=0\)
Equation de la tangente au point d'abscisse a : \(y=f'(a)(x-a)+f(a)\)
Equation de la tangente au point d'abscisse 3 : \(y=f'(3)(x-3)+f(3)\)
\(y=f'(3)(x-3)+f(3)=0(x-3)+f(3)=f(3)\)
\(f(3)=3+\frac{1}{3-2}\)
\(\iff f(3)=3+\frac{1}{1}=3+1=4\)
donc l'équation de la tangente au point d'abscisse 3 est : \(y=4\)
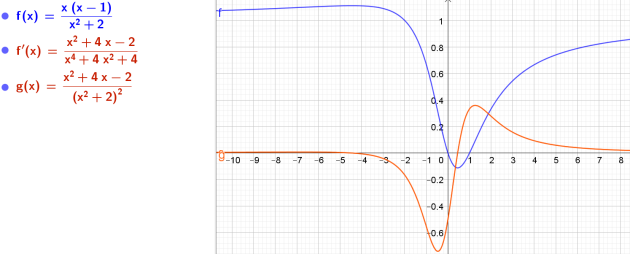
\(f\) est la fonction définie sur [-2 ;2] par \(f(x)=\frac{x(x-1)}{x^2+2}\) et soit \(\mathcal{C}\) sa courbe représentative.
Question
1.Déterminer la dérivée \(f'\) de \(f\)
Solution
\(f(x)=\frac{x(x-1)}{x^2+2}\)
\(\begin{cases}u=x(x-1)\\v=x^2+2\end{cases}\)
\((x(x-1))'=1(x-1)+x1=x-1+x=2x-1\) par la formule de dérivée d'un produit
ou \((x(x-1))'=(x^2-x)'=2x-1\)
\(\begin{cases}u'=2x-1\\v=2x\end{cases}\)
\(\frac{u}{v}=\frac{u'v-uv'}{v^2}\)
\(u'v=(2x-1)(x^2+2)=2x\times x^2+2x \times 2 -1 \times x^2 -1\times 2\)
\(\iff u'v=2x^3-x^2+4x-2\)
\(uv'=x(x-1)(2x)=2x^2(x-1)=2x^2 \times x +2x^2 \times (-1)\)
\(\iff uv'=2x^3-2x^2\)
\(u'v-uv'=(2x^3-x^2+4x-2)-(2x^3-2x^2)\)
\(\iff u'v-uv'=2x^3-x^2+4x-2-2x^3+2x^2\)
\(\iff u'v-uv'=x^2+4x-2\)
\(f'(x)=\frac{x^2+4x-2}{(x^2+2)^2}\)
2. Déterminer une équation de la tangente à \(\mathcal{C}\) aux points :
Question
\(a. O(0,f(0))\)
Solution
\(f'(0)=\frac{0^2+4\times 0-2}{(0^2+2)^2}\)
\(\iff f'(0)=\frac{-2}{(2)^2}\)
\(\iff f'(0)=\frac{-2}{4}\)
\(\iff f'(0)=\frac{-1}{2}\)
l'équation de la tangente \((T_O)\) au point O est donc de la forme :
\(y=\frac{-1}{2}x+p\)
L'ordonnée du point O est
\(y_O=f(0)=\frac{0(0-1)}{0^2+2}\)
\(\iff y_O=0\)
Comme \(O \in (T_O)\):
\(0=\frac{-1}{2}\times 0+p\)
\(\iff 0=0+p\)
\(\iff p=0\)
L'équation de la tangente \((T_O)\) est donc \(y=\frac{-1}{2}x\)
Question
\(b. A(1,f(1))\)
Solution
\(f'(1)=\frac{1^2+4\times 1-2}{(1^2+2)^2}\)
\(\iff f'(1)=\frac{1+4-2}{(1+2)^2}\)
\(\iff f'(1)=\frac{3}{9}\)
\(\iff f'(1)=\frac{1}{3}\)
l'équation de la tangente \((T_A)\) au point A est donc de la forme :
\(y=\frac{1}{3}x+p\)
L'ordonnée du point A est
\(y_A=f(1)=\frac{1(1-1)}{1^2+2}\)
\(\iff y_A=0\)
Comme \(A \in (T_A)\):
\(0=\frac{1}{3}\times 1+p\)
\(\iff 0=\frac{1}{3}+p\)
\(\iff p=-\frac{1}{3}\)
L'équation de la tangente \((T_A)\) est donc \(y=\frac{1}{3}x-\frac{1}{3}\)
Question
\(c.B(-1,f(-1))\)
Solution
\(f'(-1)=\frac{(-1)^2+4\times (-1)-2}{((-1)^2+2)^2}\)
\(\iff f'(1)=\frac{1-4-2}{(1+2)^2}\)
\(\iff f'(1)=\frac{-5}{9}\)
\(\iff f'(1)=\frac{-5}{9}\)
l'équation de la tangente \((T_B)\) au point B est donc de la forme :
\(y=\frac{-5}{9}x+p\)
L'ordonnée du point B est
\(y_B=f(-1)=\frac{-1(-1-1)}{(-1)^2+2}\)
\(\iff y_B=\frac{-1\times (-2)}{1+2}\)
\(\iff y_B=\frac{2}{3}\)
Comme \(B \in (T_B)\):
\(\frac{2}{3}=\frac{-5}{9}\times (-1)+p\)
\(\iff \frac{2}{3}=\frac{5}{9}+p\)
\(\iff \frac{5}{9}+p=\frac{2}{3}\)
\(\iff p=\frac{6}{9}-\frac{5}{9}\)
\(\iff p=\frac{1}{9}\)
L'équation de la tangente \((T_B)\) est donc \(y=\frac{-5}{9}x+\frac{1}{9}\)
Question
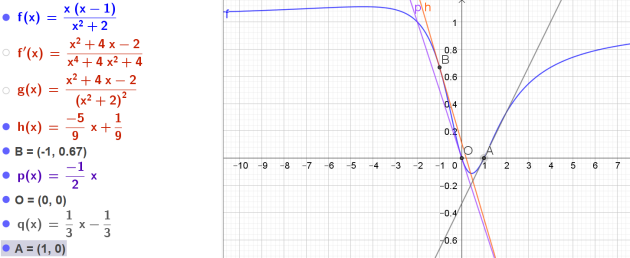
3.Tracer la courbe de la fonction \(f\) à l'aide de Geogebra et les trois tangentes déterminées précédement.
Vous imprimerez la figure et la joindrez à la copie ou me l'enverrez par Mon Bureau Numérique.
