Exercice : DM Noël 2021
Calculer les 5 premiers termes puis étudier le sens de variation des suites ci-dessous :
Question
1.\(U_n=3n-2\) pour \(n \in \mathbb{N}\)
De plus :
- Donner la nature de la suite et spécifier ces éléments caractéristiques.
- Ecrire la relation de récurrence permettant de définir \(U_n\)
Solution
\(U_0=3 \times 0-2=-2\)
\(U_1=3 \times 1-2=3-2=1\)
\(U_2=3 \times 2-2=6-2=4\)
\(U_{n+1}=3(n+1)-2=3n+3-2=3n+1\) pour \(n \in \mathbb{N}\)
\(U_{n+1}-U_{n}=(3n+1)-(3n-2)=3n+1-3n+2=3\) pour \(n \in \mathbb{N}\)
donc :
la suite \(U_n\) est arithmétique de raison 3
la suite \(U_n\) est croissante
la définition par récurrente de la suite \(U_n\) est :
\(\begin{cases}U_{n+1}=U_n+3\\U_0=-2\end{cases}\)
Question
2.\(V_n=3 \times 2^n\) pour \(n \in \mathbb{N}\)
De plus :
- Donner la nature de la suite et spécifier ces éléments caractéristiques.
- Ecrire la relation de récurrence permettant de définir \(V_n\)
Solution
\(V_{0}=3 \times 2^0=3\times 1=3\)
\(V_{1}=3 \times 2^1=3\times 2=6\)
\(V_{2}=3 \times 2^2=3\times 4=12\)
\(V_{n+1}=3 \times 2^{n+1}\) pour \(n \in \mathbb{N}\)
\(\frac{V_{n+1}}{V_{n}}=\frac{3 \times 2^{n+1}}{3 \times 2^n}=2\) pour \(n \in \mathbb{N}\)
donc :
la suite \(V_n\) est géométrique de raison 2 avec \(V_0=3>0\)
la suite \(V_n\) est croissante
la définition par récurrente de la suite \(V_n\) est :
\(\begin{cases}V_{n+1}=2V_n\\V_0=3\end{cases}\)
Question
3.\(W_n=2n^2\) pour \(n \in \mathbb{N}\)
Solution
\(W_{n+1}=2(n+1)^2=2(n^2+2n+1)\) pour \(n \in \mathbb{N}\)
\(W_{n+1}=2(n+1)^2=2n^2+4n+2\) pour \(n \in \mathbb{N}\)
\(W_{n+1}-W_n=(2n^2+4n+2)-(2n^2)=4n+2\) pour \(n \in \mathbb{N}\)
or \(n \ge 0\) pour tout \(n \in \mathbb{N}\)
\(\iff 4n \ge 0\) pour tout \(n \in \mathbb{N}\)
\(\iff 4n+2 \ge 0\) pour tout \(n \in \mathbb{N}\)
donc \(W_{n+1}-W_n\ge 0\)
La suite \(W_n\) est donc croissante pour tout \(n \in \mathbb{N}\)
Question
4.\(T_n=\frac{2}{n+1}\) pour \(n \in \mathbb{N}\)
Solution
\(T_{0}=\frac{2}{0+1}=2\)
\(T_{1}=\frac{2}{1+1}=\frac{2}{2}=1\)
\(T_{2}=\frac{2}{2+1}=\frac{2}{3}\)
\(T_{n+1}=\frac{2}{(n+1)+1}\) pour \(n \in \mathbb{N}\)
\(\iff T_{n+1}=\frac{2}{n+2}\) pour \(n \in \mathbb{N}\)
\(\frac{T_{n+1}}{T_{n}}=\frac{\frac{2}{n+2}}{\frac{2}{n+1}}\) pour \(n \in \mathbb{N}\)
\(\iff \frac{T_{n+1}}{T_{n}}=\frac{2}{n+2} \times \frac{n+1}{2}\) pour \(n \in \mathbb{N}\)
\(\iff \frac{T_{n+1}}{T_{n}}=\frac{n+1}{n+2}\) pour \(n \in \mathbb{N}\)
or \(n+1< n+2\) pour \(n \in \mathbb{N}\)
\(\iff \frac{n+1}{n+2}<1\)
\(\iff \frac{T_{n+1}}{T_{n}}<1\)
Comme \(T_{0}=2\), la suite \(T_n\) est décroissante.
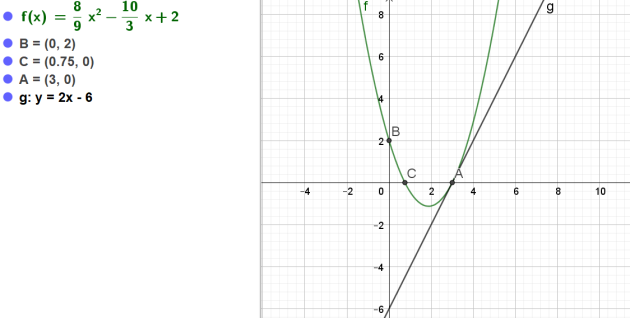
Une parabole P admet, dans un repère (O,\( \vec{i}, \vec{j}\)), une équation du type :
\(f(x)=ax^2+bx+c (a \ne 0)\)
De plus :
- P coupe l'axe des abscisses (\(Ox\)) au point A d'abscisse 3
- P coupe l'axe des ordonnées (\(Oy\)) au point B d'ordonnée 2.
- P admet au point A, la droite d'équation\( y=2x-6\)pour tangente.
Question
1. Montrer que les trois conditions précédents peuvent s'écrire sous la forme du système de 3 équations suivants :
\(\begin{cases}9a+3b+c=0\\c=2\\f'(3)=2\end{cases}\)
\(\iff \begin{cases}9a+3b=-2\\c=2\\6a+b=2\end{cases}\)
Solution
- P coupe l'axe des ordonnées (\(Oy\)) au point B d'ordonnée 2 donc \(f(0)=2\).
\(f(0)=a \times 0^2+b \times 0+c=0\)
\(\iff c=0\)
- P coupe l'axe des abscisses (\(Ox\)) au point A d'abscisse 3 donc \(f(3)=0\)
\(f(3)=a \times 3^2+b \times 3+c=0\)
\(\iff a \times 9+3b+c=0\)
\(\iff 9a+3b+c=0\)
\(\iff 9a+3b+2=0\)
\(\iff 9a+3b=-2\)
- P admet au point A, la droite d'équation\( y=2x-6\)pour tangente.
Le coefficient directeur de la tangente au point A d'abscisse \(x=3\) est
\(f'(3)\) donc \(f'(3)=2\)
\(f'(x)=2a \times x+b\)
\(f'(3)=2a \times 3+b=2\)
\(\iff 6a+b=2\)
On obtient le système suivant :
\(\begin{cases}9a+3b=-2\\c=2\\6a+b=2\end{cases}\)
Question
2.En résolvant le système :
\(\begin{cases}9a+3b=-2\\6a+b=2\end{cases}\),
déterminer les coefficients \(a,b\)
Indice
Méthode par combinaison :
\(\begin{cases}9a+3b=-2\\6a+b=2\end{cases}\)
\(\iff \begin{cases}9a+3b=-2\\18a+3b=6\end{cases}\)
En soustrayant les deux équations précédentes, montrez que :
\(9a=8\)
\(\iff a=\frac{8}{9}\)
En déduire en remplaçant par la valeur de \(a\) dans l'équation \(6a+b=2\)
que \(b=-\frac{10}{3}\)
Solution
\(c=2\)
\(\begin{cases}9a+3b=-2\\6a+b=2\end{cases}\)
\(\iff \begin{cases}9a+3b=-2\\18a+3b=6\end{cases}\)
En soustrayant les deux équations précédentes, on obtient :
\(9a=8\)
\(\iff \color{red}{a=\frac{8}{9}}\)
\(6a+b=2\)
\(6 \times \frac{8}{9}+b=2\)
\(\iff 2 \times \frac{8}{3}+b=2\)
\(\iff \frac{16}{3}+b=2\)
\(\iff \frac{16}{3}+b=\frac{6}{3}\)
\(\iff b=\frac{6}{3}-\frac{16}{3}\)
\(\iff \color{red}{b=-\frac{10}{3}}\)
Question
3. Ecrire l'expression de la parabole P
Question
4.Calculer l'abscisse du second point d'intersection de la parabole P avec l'axe des abscisses.
Solution
\(f(x)=\frac{8}{9}x^2-\frac{10}{3}x+2\)
\(\Delta=b^2-4ac\)
\(\iff \Delta=(-\frac{10}{3})^2-4 \times \frac{8}{9} \times 2\)
\(\iff \Delta=\frac{100}{9}- \frac{64}{9}\)
\(\iff \Delta=\frac{36}{9}=4\)
\(\iff \sqrt{\Delta}=2\)
\(\begin{cases}x_1=\frac{-b-\sqrt{\Delta}}{2a}\\x_2=\frac{-b+\sqrt{\Delta}}{2a}\end{cases}\)
\(\iff \begin{cases}x_1=\frac{-(-\frac{10}{3})-2}{2 \times \frac{8}{9}}\\x_2=\frac{-(-\frac{10}{3})-2}{2 \times \frac{8}{9}}\end{cases}\)
\(\iff \begin{cases}x_1=\frac{\frac{10}{3}-2}{\frac{16}{9}}\\x_2=\frac{\frac{10}{3}+2}{\frac{16}{9}}\end{cases}\)
\(\iff \begin{cases}x_1=\frac{\frac{10}{3}-\frac{6}{3}}{\frac{16}{9}}\\x_2=\frac{\frac{10}{3}+\frac{6}{3}}{\frac{16}{9}}\end{cases}\)
\(\iff \begin{cases}x_1=\frac{\frac{4}{3}}{\frac{16}{9}}\\x_2=\frac{\frac{16}{3}}{\frac{16}{9}}\end{cases}\)
\(\iff \begin{cases}x_1=\frac{4}{3} \times \frac{9}{16}}\\x_2=\frac{16}{3} \times \frac{9}{16}\end{cases}\)
\(\iff \begin{cases}x_1=\frac{3}{4}\\x_2=3\end{cases}\)
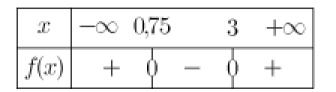
L'abscisse du second point d'intersection de la parabole P avec l'axe des abscisses est donc \(x_1=\frac{3}{4}=0,75\).
Question
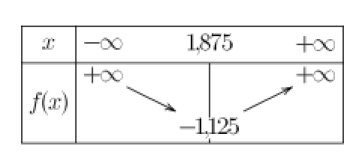
5.Dresser le tableau de signes de la fonction représentée par la parabole P
Question
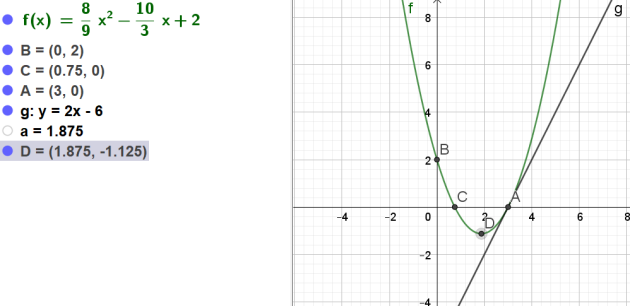
6.Dresser le tableau de variations de la fonction représentée par la parabole P
Solution
\(\alpha=\frac{x_1+x_2}{2}=\frac{0,75+3}{2}=\frac{3,75}{2}=1,875\)
\(\color{magenta}{\text{2ème méthode}}\)
\(\alpha=\frac{-b}{2a}\)
\(\iff \alpha=\frac{-(-\frac{10}{3})}{2\times (\frac{8}{9})}\)
\(\iff \alpha=\frac{\frac{10}{3}}{\frac{16}{9}}\)
\(\iff \alpha=\frac{10}{3} \times \frac{9}{16}\)
\(\iff \alpha=\frac{5}{1} \times \frac{3}{8}\)
\(\iff \alpha=\frac{15}{8}=1,875\)
\(\beta=f(\alpha)=\frac{8}{9} \times \frac{225}{64}-\frac{150}{24}+2\)
\(\iff \beta=f(\alpha)=\frac{25}{8}-\frac{150}{24}+2\)
\(\iff \beta=f(\alpha)=\frac{75}{24}-\frac{150}{24}+\frac{48}{24}\)
\(\iff \beta=f(\alpha)=-\frac{27}{24}=-\frac{9}{8}=-1,125\)
.
Question
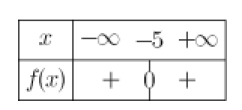
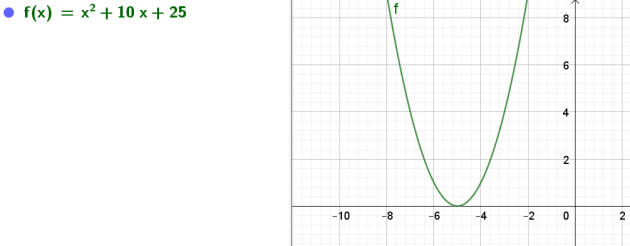
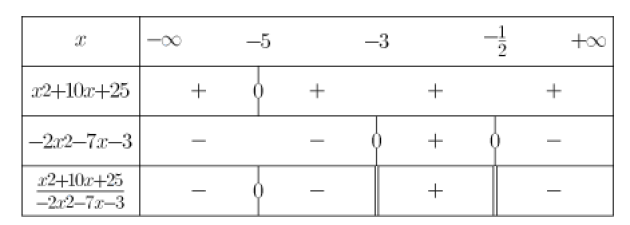
1.Etudier le signe de \(x^2+10x+25\) (dresser un tableau de signes)
Question
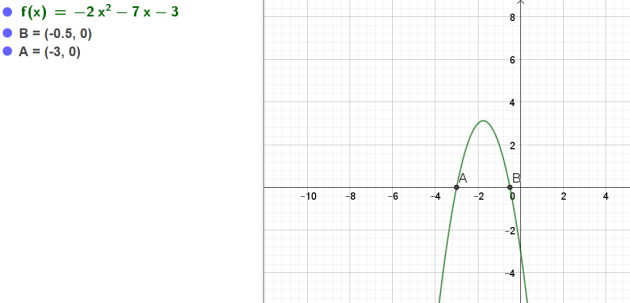
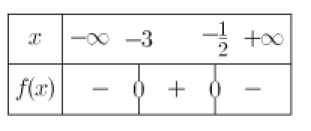
2.Etudier le signe de \(-2x^2-7x-3\) (dresser un tableau de signes)
Solution
\(-2x^2-7x-3\)
\(\Delta=b^2-4ac\)
\(\iff \Delta=(-7)^2-4 \times (-2) \times (-3)\)
\(\iff \Delta=49-24=25\)
\(\iff \sqrt{\Delta}=5\)
\(\begin{cases}x_1=\frac{-b-\sqrt{\Delta}}{2a}\\x_2=\frac{-b+\sqrt{\Delta}}{2a}\end{cases}\)
\(\iff \begin{cases}x_1=\frac{-(-7)-5}{2 \times (-2)}\\x_2=\frac{-(-7)+5}{2 \times (-2)}\end{cases}\)
\(\iff \begin{cases}x_1=\frac{7-5}{-4}\\x_2=\frac{7+5}{-4}\end{cases}\)
\(\iff \begin{cases}x_1=\frac{2}{-4}\\x_2=\frac{12}{-4}\end{cases}\)
\(\iff \begin{cases}x_1=-\frac{1}{2}\\x_2=-3\end{cases}\)
Comme \(a\)<0 :
Question
Question
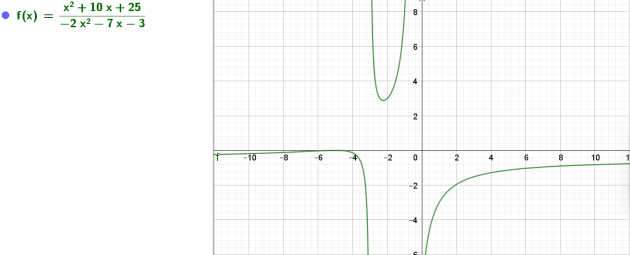
4. En déduire les solutions de \(\frac{x^2+10x+25}{-2x^2-7x-3}\le 0\)
Solution
Les solutions de \(\frac{x^2+10x+25}{-2x^2-7x-3}\le 0\)
sont donc \(]-\infty ;-3[ \cup ]-\frac{1]{2} ;+\infty[\)
Dériver les fonctions définies ci-dessous :
Donner les ensembles de définition des fonctions et de leurs dérivées.
Question
Question
2. \(g(x) = (2x + 3)(3x - 7)\)
Indice
\((u \times v)'=u' \times v+ u \times v'\)
Solution
\(u=2x+3 \mapsto u'=2\)
\(v=3x-7 \mapsto v'=3\)
\(g'(x) = 2(3x - 7)+(2x+3) \times 3\)
\(\iff g'(x) = 6x - 14+6x+9\)
\(\iff g'(x) = 12x -5\)
\(D_g=D_{g'}=\mathbb{R}\) car les fonctions \(g\) et \(g'\) sont des fonctions polynômes.
Question
\(3. h(x) = \frac{2x+4}{3x-1}\)
Indice
\((\frac{u}{v})'=\frac{u'v-uv'}{v^2}\)
Solution
\(u=2x+4 \mapsto u'=2\)
\(v=3x-1\mapsto v'=3\)
\(h'(x)=\frac{2(3x-1)-(2x+4) \times 3}{(3x-1)^2}\)
\(\iff h'(x)=\frac{(6x-2)-(6x+12)}{(3x-1)^2}\)
\(\iff h'(x)=\frac{6x-2-6x-12}{(3x-1)^2}\)
\(\iff h'(x)=\frac{-14}{(3x-1)^2}\)
\(3x-1=0\)
\(\iff 3x=1\)
\(\iff x=\frac{1}{3}\)
\(D_h=D_{h'}=\mathbb{R}\\\){\(\frac{1}{3}\)}
Question
4\(.l(x) =\sqrt{x}(1-\frac{1}{x})\)
Indice
\(( u \times v)'=u' \times v + u \times v'\)
\((\sqrt{x})'=\frac{1}{2\sqrt{x}}\)
\((\frac{1}{x})'=\frac{-1}{x^2}\)
Solution
\(u=\sqrt{x} \mapsto u'=\frac{1}{2\sqrt{x}}\)
\(v=1-\frac{1}{x} \mapsto v'=\frac{1}{x^2}\)
\(l'(x) =\frac{1}{2\sqrt{x}}(1-\frac{1}{x})+ \sqrt{x} \times \frac{1}{x^2}\)
\(\iff l'(x) =\frac{\sqrt{x}}{2x}(1-\frac{1}{x})+ \sqrt{x} \times \frac{1}{x^2}\)
\(\iff l'(x) =\frac{\sqrt{x}}{2x}-\frac{\sqrt{x}}{2x^2}+ \frac{\sqrt{x}}{x^2}\)
\(\iff l'(x) =\frac{\sqrt{x}}{2x}+\frac{\sqrt{x}}{2x^2}\)
\(\iff l'(x) =\frac{x\sqrt{x}}{2x^2}+\frac{\sqrt{x}}{2x^2}\)
\(\iff l'(x) =\frac{x\sqrt{x}+\sqrt{x}}{2x^2}\)
\(\iff l'(x) =\frac{(x+1)\sqrt{x}}{2x^2}\)
\(D_l=D_{l'}=\mathbb{R}^+_*\)
car une racine carrée est définie sur \(\mathbb{R}^+\) et une fonction inverse est définie sur \(\mathbb{R}_*\)
Question
5\(.m(x) =\frac{x+5}{x^2+1}\)
Indice
\((\frac{u}{v})'=\frac{u'v-uv'}{v^2}\)
Solution
\((\frac{u}{v})'=\frac{u'v-uv'}{v^2}\)
\(u=x+5 \mapsto u'=1\)
\(v=x^2+1 \mapsto v'=2x\)
\(m'(x)=\frac{1 \times (x^2+1)-(x+5) \times 2x}{(x^2+1)^2}\)
\(\iff m'(x)=\frac{(x^2+1)-(2x^2+10x)}{(x^2+1)^2}\)
\(\iff m'(x)=\frac{x^2+1-2x^2-10x}{(x^2+1)^2}\)
\(\iff m'(x)=\frac{-x^2-10x+1}{(x^2+1)^2}\)
\(D_m=D_{m'}=\mathbb{R}\)
car \(x^2+1=0 \iff x^2=-1\) est impossible
en effet un nombre réel au carré est toujours positif.
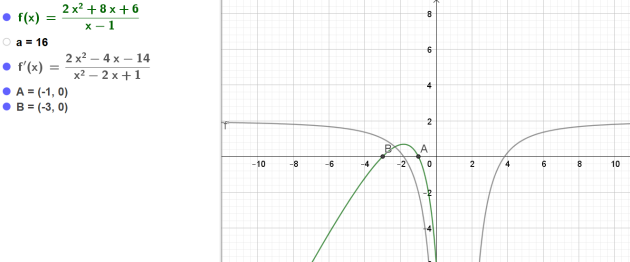
Soit \(f\) la fonction définie par \(f(x) =\frac{2x^2+8x+6 }{x-1}\)
On note \(C_f\) sa représentation graphique.
Question
1.Montrer que la fonction dérivée \(f'\) de la fonction \(f\) est \(f'(x) =\frac{2x^2-4x-14}{(x-1)^2}\)
On spécifiera les ensembles de définition des fonctions \(f\) et \(f'\)
Solution
\((\frac{u}{v})'=\frac{u'v-uv'}{v^2}\)
\(u=2x^2+8x+6 \mapsto u'=4x+8\)
\(v=x-1 \mapsto v'=1\)
\(f'(x) =\frac{(4x+8) \times (x-1) -(2x^2+8x+6) \times 1}{(x-1)^2}\)
\(\iff f'(x) =\frac{(4x^2-4x+8x-8) -(2x^2+8x+6) }{(x-1)^2}\)
\(\iff f'(x) =\frac{4x^2+4x-8 -2x^2-8x-6 }{(x-1)^2}\)
\(\iff f'(x) =\frac{2x^2-4x-14 }{(x-1)^2}\)
\(D_f=D_{f'}=\mathbb{R}\\\){1}
car \(x-1=0 \iff x=1\)
Question
2. Soit A et B les points d'intersection de la courbe représentant la fonction f : \(C_f\) et l'axe des abscisses.
Calculer les coordonnées des points A et B, puis les équations des tangentes \(T_A\) et \(T_B\) à la courbe \(C_f\) aux points A et B.
Solution
\(f(x) =\frac{2x^2+8x+6 }{x-1}=0\)
\(\iff 2x^2+8x+6=0\)
\(\Delta=b^2-4ac\)
\(\iff \Delta=8^2-4 \times 2 \times 6\)
\(\iff \Delta=64-48=16\)
\(\iff \sqrt{\Delta}=4\)
\(\begin{cases}x_1=\frac{-b-\sqrt{\Delta}}{2a}\\x_2=\frac{-b+\sqrt{\Delta}}{2a}\end{cases}\)
\(\iff \begin{cases}x_1=\frac{-8-4}{2 \times 2}\\x_2=\frac{-8+4}{2 \times 2}\end{cases}\)
\(\iff \begin{cases}x_1=\frac{-12}{4}\\x_2=\frac{-4}{4}\end{cases}\)
\(\iff \begin{cases}x_1=-3\\x_2=-1\end{cases}\)
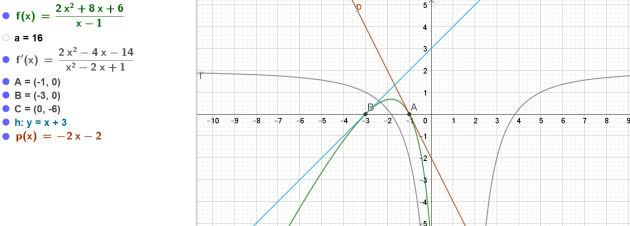
Equation de la tangente \(T_B\) à la courbe \(C_f\) au point B(-3 ;0) :
\(y=f'(x_B)(x-x_B)+f(x_B)\)
\(f'(x_B) =\frac{2 \times (-3)^2-4 \times (-3)-14 }{(-3-1)^2}\)
\(\iff f'(x_B) =\frac{2 \times 9+12-14 }{(-4)^2}\)
\(\iff f'(x_B) =\frac{18+12-14 }{16}\)
\(\iff f'(x_B) =\frac{16 }{16}=1\)
\(\iff y=1(x-(-3))+0\)
\(\iff y=x+3\)
Equation de la tangente \(T_A\) à la courbe \(C_f\) au point A(-1 ;0) :
\(y=f'(x_A)(x-x_A)+f(x_A)\)
\(f'(x_A) =\frac{2 \times (-1)^2-4 \times (-1)-14 }{(-1-1)^2}\)
\(\iff f'(x_A) =\frac{2 \times 1+4-14 }{(-2)^2}\)
\(\iff f'(x_B) =\frac{2+4-14 }{4}\)
\(\iff f'(x_B) =\frac{-8 }{4}=-2\)
\(\iff y=-2(x-(-1))+0\)
\(\iff y=-2(x+1)\)
\(\iff y=-2x-2\)
Question
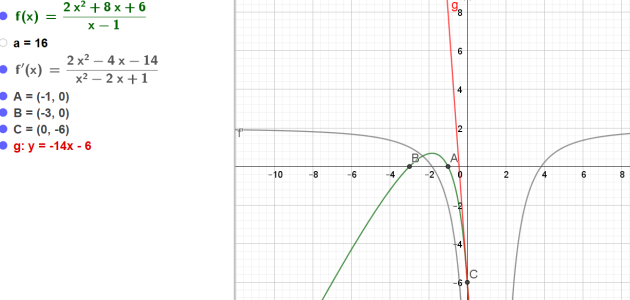
3. Soit C le point d'intersection de \(C_f\) avec l'axe des ordonnées.
Calculer les coordonnées du point C, puis une équation de la tangente \(T_C\) à la courbe \(C_f\) au point C.
Solution
\(f(0) =\frac{2 \times 0^2+8 \times 0+6 }{0-1}\)
\(\iff f(0) =\frac{6 }{-1}=-6\)
Le point C, point d'intersection de \(C_f\) avec l'axe des ordonnées
a donc pour coordonnées (0 ;-6)
Equation de la tangente \(T_C\) à la courbe \(C_f\) au point C :
\(y=f'(x_C)(x-x_C)+f(x_C)\)
\(f'(x_C) =\frac{2 \times 0^2-4 \times 0-14 }{(0-1)^2}\)
\(\iff f'(x_C) =\frac{-14 }{(-1)^2}\)
\(\iff f'(x_C) =-14\)
\(\iff y=-14(x-0)+(-6)\)
\(\iff y=-14x-6\)
Question
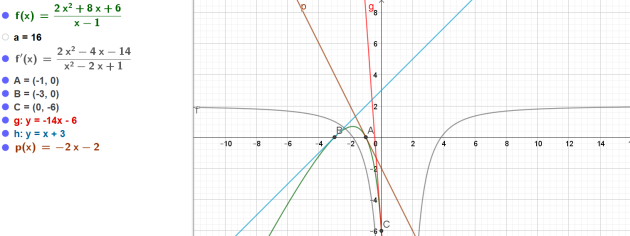
4. Tracer sur un même repère les tangentes \(T_A\),\(T_B\) et \(T_C\) ainsi que la courbe \(C_f\).
On tracera la fonction pour \(x \in [-6 ;0]\) et \(y \in [-8 ;4]\)
On prendra 1 cm pour l'unité en abscisse.
On prendra 1 cm pour l'unité en ordonnée.