Exercice : Complet 1
On considère une fonction \(f\) définie et dérivable sur l'intervalle [0 ; 2,5].
On note \(f'\) la fonction dérivée de la fonction \(f\) .
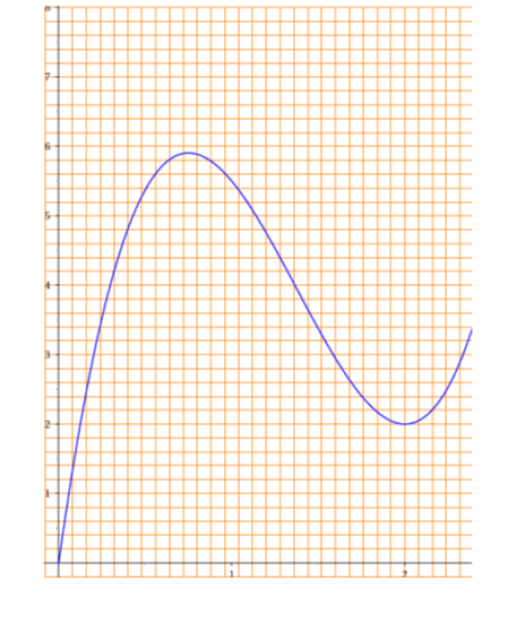
On donne en annexe, la courbe représentative de la fonction \(f\) , appelée C , dans un repère orthogonal.
La courbe \(C_f\) possède les propriétés suivantes :
– la courbe \(C_f\) passe par le point A(1 ; 5,5) ;
– la courbe \(C_f\) passe par le point B(2 ; 2) ;
– la tangente en B à la courbe \(C_f\) est horizontale ;
– la tangente en A à la courbe \(C_f\) passe par le point T (0 ; 8,5).
Question
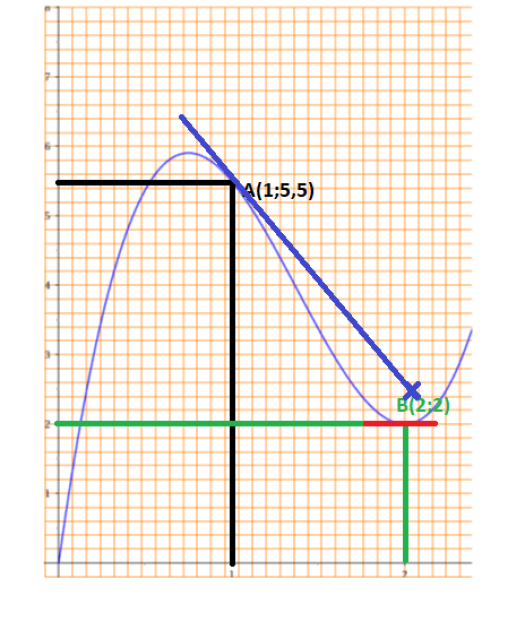
1. Placer les points A, B et T et tracer les tangentes à la courbe \(C_f\) en A et B.
Question
2. Déterminer\( f (1), f (2)\), \(f ′(2) \)et \(f'(1)\)
Solution
La fonction \(f\) passe par le point (1;5,5) donc \(f(1)=5,5\)
La fonction \(f\) passe par le point (2;2) donc \(f(2)=2\)
\(f'(2)=0\) car la tangente en \(x=2\) est horizontale.
\(f'(1)=\frac{5,5-8,5}{1-0}=\frac{-3}{1}=-3\) donc \(f'(1)=-3\)
Question
4. Donner par lecture graphique une valeur approchée de la deuxième solution de l'équation
\(f ′(x) = 0.\)
Solution
\(x=0,75 \)car la tangente est horizontale en cette abscisse.
La fonction f dont on connaît la courbe C est définie sur l'intervalle [0 ; 2,5] par :
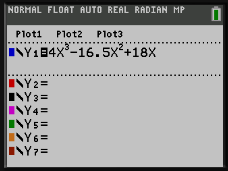
\(f (x) = 4x^3 −16,5x^2 +18x.\)
Question
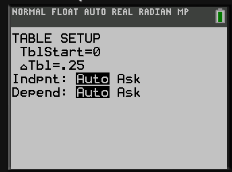
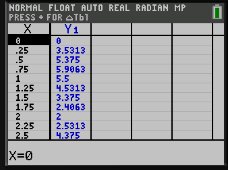
1. Reproduire et compléter le tableau de valeurs suivant à l'aide de la calculatrice.
\(x\) | 0 | 0,5 | 0,75 | 1 | 1,5 | 2 | 2,5 |
|---|---|---|---|---|---|---|---|
\(f(x)\) |
Question
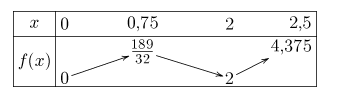
2.Dresser le tableau de variations de la fonction \(f\)
Solution
\(f (0) = 4\times 0^3 −16,5 \times 0^2 +18 \times 0=0-0+0=0\)
\(f (\frac{3}{4}) = 4\times (\frac{3}{4})^3 −16,5\times (\frac{3}{4})^2 +18 \times \frac{3}{4}.\)
\(\iff f (\frac{3}{4}) = 4\times \frac{27}{64} −16,5\times \frac{9}{16} +18 \times \frac{3}{4}.\)
\(\iff f (\frac{3}{4}) =\frac{27}{16} −165\times \frac{9}{160} +9 \times \frac{3}{2}.\)
\(\iff f (\frac{3}{4}) =\frac{27}{16} −165\times \frac{9}{160} +\frac{27}{2}.\)
\(\iff f (\frac{3}{4}) =\frac{27}{16} −33\times \frac{9}{32} +\frac{27}{2}.\)
\(\iff f (\frac{3}{4}) =\frac{27}{16} −\times \frac{297}{32} +\frac{27}{2}.\)
\(\iff f (\frac{3}{4}) =\frac{54}{32} −\times \frac{297}{32} +\frac{432}{32}.\)
\(\iff f (\frac{3}{4}) =\frac{189}{32}.\)
Question
2. a. Calculer \(f ′(x).\)
Solution
\(f'(x) = 4 \times 3x^2 −16,5 \times 2x +18\)
\(\iff f'(x) = 12x^2 −33x +18\)
Question
b. Montrer que :
\(f ′(x) = 12(x −2)(x −0,75).\)
Solution
\(\Delta=b^2-4ac=(-33)^2-4\times 12 \times 18\)
\(\iff \Delta=b^2-4ac=1089-864=225\)
\(\begin{cases}x_1=\frac{-b-\sqrt{\Delta}}{2a}\\\x_2=frac{-b+\sqrt{\Delta}}{2a}\end{cases}\)
\(\iff \begin{cases}x_1=\frac{-(-33)-\sqrt{225}}{2\times 12}\\x_2=\frac{-(-33)+\sqrt{225}}{2\times 12}\end{cases}\)
\(\iff \begin{cases}x_1=\frac{33-15}{24}\\x_2=\frac{33+15}{24}\end{cases}\)
\(\iff \begin{cases}x_1=\frac{18}{24}\\x_2=\frac{48}{24}\end{cases}\)
\(\iff \begin{cases}x_1=\frac{3}{4}\\x_2=2\end{cases}\)
La forme factorisée est donc :
\(f'(x)= a(x-x_1)(x-x_2)\)
\(\iff f'(x)= 12(x-2)(x-0,75)\)
Question
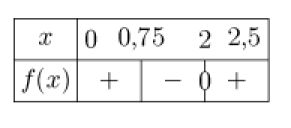
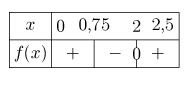
c. Étudier le signe de \(f ′(x)\) suivant les valeurs de \(x\) sur l'intervalle [0 ; 2,5] à l'aide d'un tableau de signe.
Question
3.Quel lien existe-t-il entre les variations de la fonction \(f\) et le signe de sa dérivée.
Solution

\(\color{red}{Théorème : }\)
Soit une fonction f définie et dérivable sur un intervalle I.
- Si \(\color{magenta}{f'(x) \le 0}\), alors \(f\) est décroissante sur I.
- Si \(\color{magenta}{f'(x) \ge 0}\) , alors \(f\) est croissante sur I.