Exercice : (2x-5)/(3-4x)
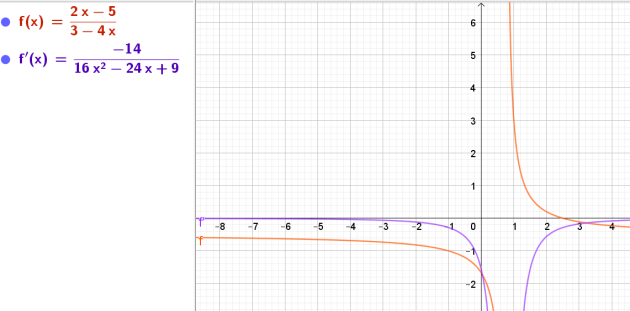
Soit \(g\) la fonction définie sur \(]\frac{3}{4} ;+\infty[\) par \(g(x)=\frac{2x-5}{3-4x}\)
Question
1.Montrer que sa dérivée \(g'\) est définie par :
\(g'(x)=-\frac{14}{(3-4x)^2}\) pour tout \(x \in ]\frac{3}{4} ;+\infty[\)
Indice
\(x\mapsto 1\)
\(\frac{u}{v} \mapsto \frac{u'v-uv'}{v^2}\)
\(k \mapsto 0\)
\(ku \mapsto ku'\)
\(u+v\mapsto u'+v'\)
Solution
\(\begin{cases}u=2x-5\\v=3-4x\end{cases}\)
\(\begin{cases}u'=2\\v'=-4\end{cases}\)
\(g'(x)=\frac{2 \times (3-4x)-(2x-5)\times (-4)}{(3-4x)^2}\)
\(\iff g'(x)=\frac{6-8x-(-8x+20)}{(3-4x)^2}\)
\(\iff g'(x)=\frac{6-8x-+8x-20}{(3-4x)^2}\)
\(\iff g'(x)=\frac{-14}{(3-4x)^2}\)
Question
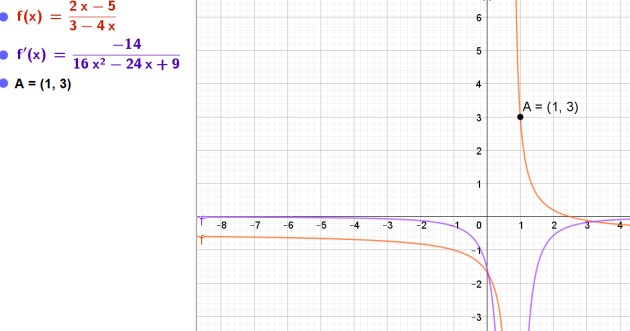
2.Montrer que le point A(1;3) appartient à la courbe de \(g\) : \(C_g\)
Solution
\(g(1)=\frac{2\times 1-5}{3-4 \times 1}\)
\(\iff g(1)=\frac{2-5}{3-4}\)
\(\iff g(1)=\frac{-3}{-1}=3\)
donc le point A(1;3) appartient à la courbe de \(g\): \(C_g\)
Question
3.Montrer que le nombre dérivé de \(g\) en 1 est -14
Solution
\(g'(1)=\frac{-14}{(3-4 \times 1)^2}\)
\(\iff g'(1)=\frac{-14}{(-1)^2}\)
\(\iff g'(1)=\frac{-14}{1}=-14\)
Question
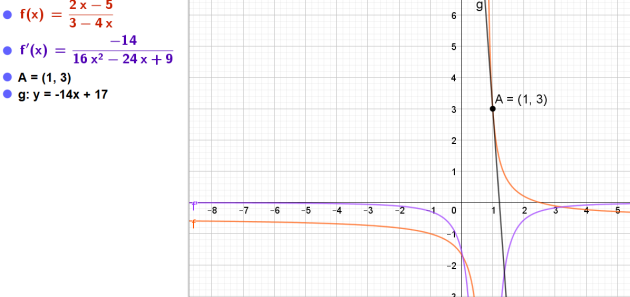
4.Déduire des questions précédentes une équation de la tangente à \(C_g\) en A : \(T_a\)
Solution
\(y=f'(1)(x-1)+f(1)\)
\(\iff y=-14(x-1)+3\)
\(\iff y=-14x+14+3\)
\(\iff y=-14x+17\)
L'équation de la tangente au point A est donc \(y=-14x+17\)
