Exercice : 1/x
Partie A
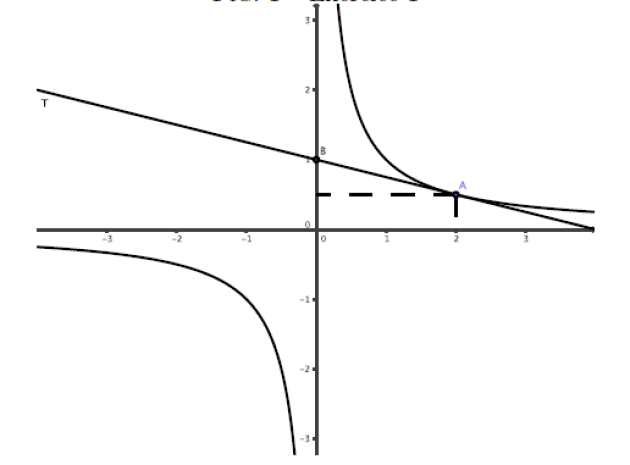
La droite T passe par le point A d'abscisse 2 de la courbe \(C_f\) et par le point d'ordonnée 1 de l'axe des ordonnées.
Question
1. Déterminer l'équation réduite de la droite T.
Solution
Calcul du coefficient directeur de la droite (AB):
\(a=\frac{y_A-y_B}{x_A-x_B}\)
\(\iff a=\frac{f(2)-1}{2-0}\)
\(\iff a=\frac{\frac{1}{2}-1}{2}\)
\(\iff a=-\frac{1}{4}\)
Calcul de l'ordonnée à l'origine de la droite (AB) :
\(y=ax+b\)
B(0,1) \(\in\) (AB)
\(\iff 1=a \times 0+b\)
\(\iff 1=b\)
\(\iff b=1\)
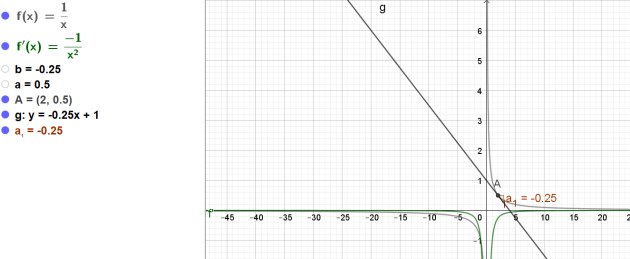
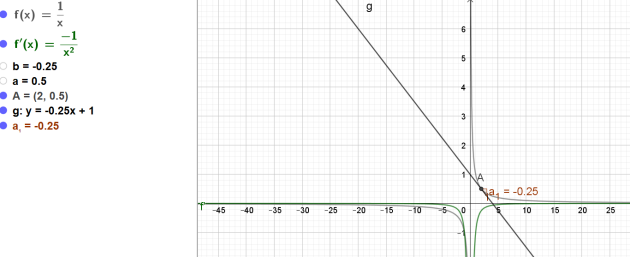
L'équation de la droite T est donc \(y=-0,25x+1\)
Question
2. Calculer le quotient
\(\frac{f(2 + h) − f(2)}{h}\)
\(h\) désignant un nombre réel non nul appartenant à l'intervalle ] − 2; 2[.
En déduire \(f'(2)\)
Solution
\(\frac{f(2 + h) − f(2)}{h}\)
\(=\frac{\frac{1}{2 + h} − \frac{1}{2}}{h}\)
\(=\frac{\frac{2}{2(2 + h)} −\frac{2+h}{2(2+h)}}{h}\)
\(=\frac{\frac{-h}{2(2 + h)}{h}\)
\(f'(2)=\)\(\frac{\frac{-1}{2 \times 2}=\frac{-1}{4}\)
Partie B
.
Question
Question
2. Déterminer une équation de la tangente à la courbe représentative de \(f\), \(C_f\) , en son point d'abscisse 2.