Exercice : Variations 7
On appelle \(f\) la fonction définie sur \(\mathbf{R}^{*}\) par \(f(x)=\frac{1}{x^{2}}\).
Question
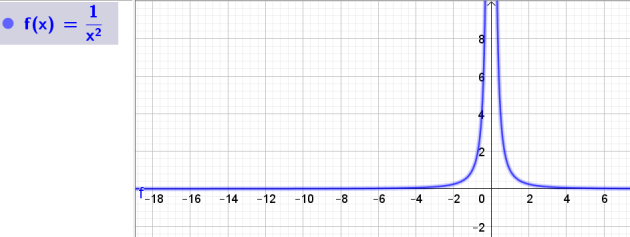
1. Grâce au logiciel Geogebra, on a tracer le graphe de la fonction \(f\),
déterminer quelles \(\textit{semblent}\) être les variations de \(f\) sur son domaine de définition ?
Solution
La fonction \(f\) semble être croissante sur \(]-\infty;0[\) et décroissante sur l'intervalle \(]0;+\infty[\).
Question
2. Montrer que pour tous réels a et b non nuls, \(f(b)-f(a)=\frac{(a-b)(a+b)}{a^{2}b^{2}}\)
Solution
\(f(b)-f(a)=\frac{1}{b^{2}}-\frac{1}{a^{2}}\)
\(\iff f(b)-f(a)=\frac{a^2}{a^2b^{2}}-\frac{b^2}{a^{2}b^2}\)
\(\iff f(b)-f(a)=\frac{a^2-b^2}{a^{2}b^2}\)
\(\iff f(b)-f(a)=\frac{(a-b)(a+b)}{a^{2}b^2}\)
Question
3. En déduire les variations de f sur \(\mathbf{R}_{+}^{*}.\)
Indice
Montrer que si \(0<a<b\) alors \(f(a)<f(b)\)
Solution
Si \(0<a<b\) alors \(0<(a+b)\)
Si \(0<a<b\) alors \(-b<a-b<0\)
\(a^2>0\) et \(b^2>0\)
donc
Si \(0<a<b\) alors \(\frac{(a-b)(a+b)}{a^{2}b^2}<0\)
donc
Si \(0<a<b\) alors \(f(a)-f(b)<0\)
donc
Si \(0<a<b\) alors \(f(a)<f(b)\)
La fonction \(f\) est décroissante sur \(\mathbf{R}_{+}^{*}.\)