Exercice : Variations 2
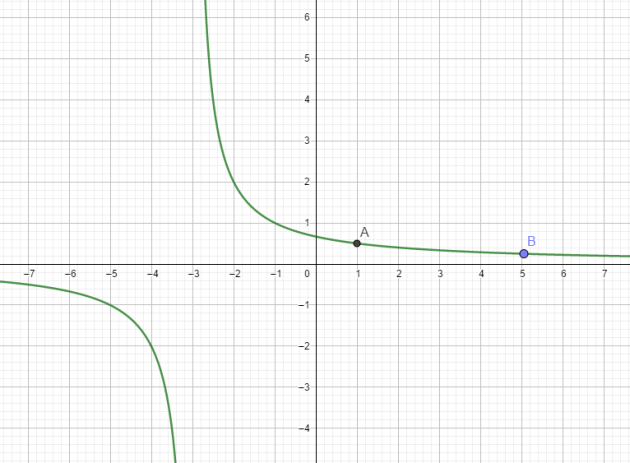
On appelle \(f\) la foncion définie pour tout \(x \ne −3\) par \(f(x) =\frac{2}{x + 3}\)
Question
1. Prouver que pour tous réels a et b de \(\mathbb{R}\)\{-3} :\( f(b) − f(a) = \frac{2(a − b)}{(a + 3)(b + 3)}\)
Solution
\(f(b) − f(a)\)
\(= \frac{2}{b + 3}-\frac{2}{a + 3}\)
\(= \frac{2(a+3)}{(a+3)(b +3)}-\frac{2(b+3)}{(a + 3)(b+3)}\)
\(= \frac{2a+6-2b-6}{(a + 3)(b+3)}\)
\(= \frac{2a-2b}{(a + 3)(b+3)}\)
\(=\frac{2(a − b)}{(a + 3)(b+3)}\)
Question
b. En déduire les variations de f sur ] − 3;+∞[ puis sur ] −∞;−3[
Solution
Si \(a \in ] − 3;+∞[\) et \(b \in ] − 3;+∞[\) et a<b :
\((a + 3)>0\) et \((b+3)>0\) a-b<0
donc \(f(b)-f(a)=\frac{2(a − b)}{(a + 3)(b+3)}<0\)
La fonction f est donc décroissante sur ] − 3;+∞[
Si \(a \in ] −∞ ;-3[\) et \(b \in ] −∞ ;-3[\) et a<b :
\((a + 3)<0\) et \((b+3)<0\) a-b<0
donc \(f(b)-f(a)=\frac{2(a − b)}{(a + 3)(b+3)}<0\)
La fonction f est donc décroissante sur ]-∞ ;-3[