Exercice : Condition Courbe 3
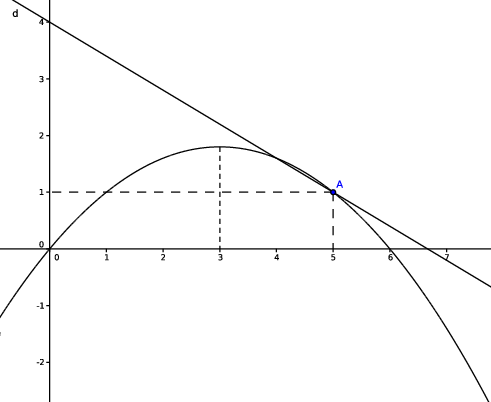
Le graphique ci-dessous comporte:
une droite d passant par les points de coordonnées respectives (0;4) et (5;1);
la courbe représentative d'une fonction \(f\) définie par \(f(x)=ax^{2}+bx+c\),a, b et c désignant trois nombres réels.
Le but principal de l'exercice est de calculer les nombres réels a, b et c, sachant que:
la courbe représentative de la fonction f passe par les points de coordonnées respectives (0;0) et (5;1);
le maximum de la fonction f est atteint pour \(x\)=3.
Question
1. Déterminer le coefficient directeur puis l'équation réduite de la droite (d).
Solution
Calcul du coefficient directeur :
La droite passe par les points (0;4) et (5;1);
a=\frac{1-4}{5-0}=\frac{-3}{5}=-0,6
L'équation de la droite (d) est donc de la forme
\(y=-0,6x+b\)
Calcul de l'ordonnée à l'origine
La droite passe par le point (0;4)
donc \(4=-0,6\times 0+b\)
\(\iff 4=b\)
\(\iff b=4\)
ou
La droite passe par le point (5;1)
donc \(1=-0,6\times 5+b\)
\(\iff 1=-3+b\)
\(\iff b=1-(-3)\)
\(\iff b=1+3=4\)
L'équation de la droite (d) est donc \(y=-0,6x+4\)
Question
2. (a) Justifier l'égalité \(f(0)=0\).
Solution
La courbe de la fonction \(f\) passe par l'origine du repère donc \(f(0)=0\)
Question
(b) Montrer que c=0.
Solution
\(f(0)=a\times 0^{2}+ b\times 0+c=c=0\) donc c=0
et \(f(x)=ax^{2}+ bx\)
Question
3. Déterminer graphiquement le nombre réel \(f(5)\).
En déduire que \(25a+5b=1.\)
Solution
Graphiquement \(f(5)=1\)
donc \(f(5)=a\times 5^{2}+ b\times 5=1\)
\(\iff f(5)=25a+5b=1\)
Question
4. Déterminer la valeur du nombre réel \(\frac{-b}{2a}\).
En déduire que \(6a+b=0.\)
Solution
L'abscisse du sommet de la parabole est 3
donc
\(\frac{-b}{2a}=3\)
\(\iff -b=6a\)
\(\iff 6a+b=0\)
Question
5. Grâce aux deux équations précédentes, calculer les nombres réels a et b.
Solution
\(\begin{cases}25a+5b=1\\6a+b=0\end{cases}\)
\(\iff \begin{cases}25a+5b=1\\30a+5b=0\end{cases}\)
\(5a=-1\) (\(L_2-L_1\))
\(a=-\frac{1}{5}=-0,2\) Ce qui est logique vu le sens de variation de la fonction \(f.\)
et
\(6\times (-\frac{1}{5})+b=0\)
\(\iff -\frac{6}{5}+b=0\)
\(\iff b=\frac{6}{5}=1,2\)
\(f(x)=-0,2x^{2}+ 1,2x\)
Question
6. Résoudre l'équation\(-0,6x+4=-0,2x^{2}+1,2x\).Interpréter graphiquement les valeurs obtenues.
Solution
Résoudre l'équation\(-0,6x+4=-0,2x^{2}+1,2x\) revient à chercher l'abscisse du point d'intersection de la droite (d)
et de la parabole représentant la fonction \(f\)
\(-0,6x+4=-0,2x^{2}+1,2x\)
\(\iff 0,2x^{2}-0,6x+4=1,2x\)
\(\iff 0,2x^{2}-0,6x-1,2x+4=0\)
\(\iff 0,2x^{2}-1,8x+4=0\)
\(\Delta=b^2-4ac\)
\(\iff \Delta=(-1,8)^2-4\times 0,2 \times 4\)
\(\iff \Delta=3,24-3,2=0,04\)
\(\begin{cases}x_1=\frac{-b-\sqrt{\Delta}}{2a}\\x_2=\frac{-b+\sqrt{\Delta}}{2a}\end{cases}\)
\(\iff \begin{cases}x_1=\frac{-(-1,8)-\sqrt{0,04}}{2\times 0,2}\\x_2=\frac{-(-1,8)+\sqrt{0,04}}{2 \times 0,2}\end{cases}\)
\(\iff \begin{cases}x_1=\frac{1,8-0,2}{0,4}\\x_2=\frac{1,8+0,2}{0,4}\end{cases}\)
\(\iff \begin{cases}x_1=\frac{1,6}{0,4}\\x_2=\frac{2}{0,4}\end{cases}\)
\(\iff \begin{cases}x_1=4\\x_2=5\end{cases}\)
La droite (d) et la parabole représentant la fonction \(f\) ont donc deux points d'intersection
\((4,f(4))\) et \((5,f(5))\)
or
\(f(4)=-0,2\times 4^{2}+1,2 \times 4=-0,2\times 16+4,8=-3,2+4,8=1,6\)
ou
\(-0,6\times 4+4=-2,4+4=1,6\)
\(f(5)=-0,2\times 5^{2}+1,2 \times 5=-0,2\times 25+6=-5+6=1\)
ou
\(-0,6\times 5+4=-3+4=1\)
La droite (d) et la parabole représentant la fonction \(f\) ont donc deux points d'intersection \((4;1,6)\) et \((5;1)\)