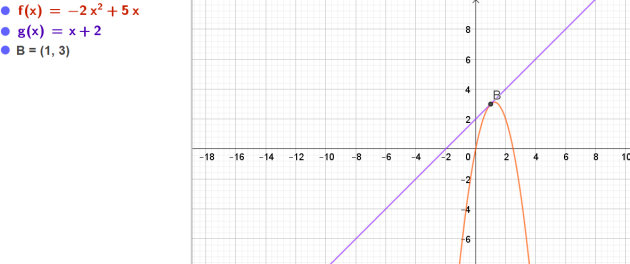
Exercice : Condition Courbe 2
\(f\) est une fonction définie sur \(\mathbb{R}\) par
\(f(x)=ax^2+bx\)
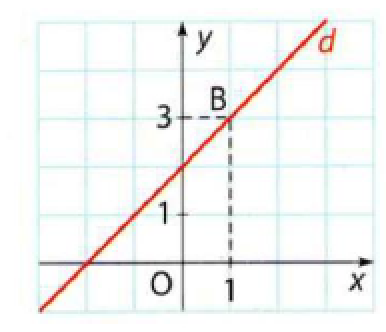
B est le point de coordonnées (1;3)
La droite (d) d'équation \(y=x+2\) est tangente à la courbe \(C_f\)en B à la courbe représentative de \(f\).
Question
1.Démontrer que \((d) \)est tangente en B à \(C_f\) équivaut à \(f(1)=3\) et \(f'(1)=1\)
Solution
La droite d'équation \(y=x+2\) est tangente à la courbe au point B d'abscisse 1 donc \(f'(1)=1\)
car le coefficient directeur de la droite (d) vaut 1.
\(f(1)=3\) car le point B à pour coordonnées (1,3)
Question
2.Déduisez en les valeurs de a et b et l'expression de la fonction \(f\)
Solution
\(f'(x)=a\times 2x+b \times 1\)
\(f'(x)=2ax+b\)
\(f'(1)=2a+b=1\)(1)
\(f(1)=a\times 1^2+b \times 1=3\)
\(\iff f(1)=a+b=3\)(2)
\(a=1-3=-2\) (L1-L2)
\(-2+b=3\)
donc \(b=5\)
L'expression de la fonction \(f\) est donc \(f(x)=-2x^2+5x\)
