Exercice : Tangente 4
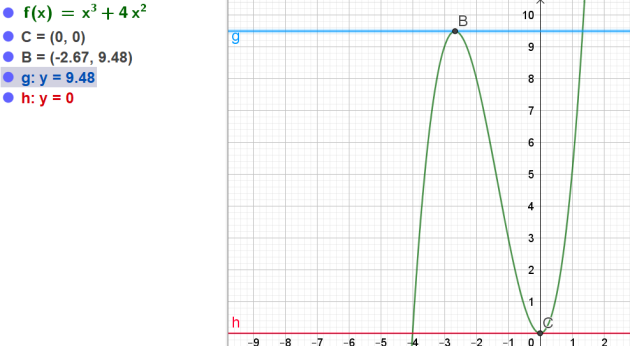
Soit \(C_p\) sa courbe représentant la fonction p définie sur \(\mathbb{R}\) par \(p(x)=x^3+4x^2\)
Question
Existe t il des points de \(C_p\) où la tangente est parallèle à l'axe des abscisses ?Si oui, lesquels ?
Solution
\(p'(x)=3x^2+4 \times 2x\)
\(\iff p'(x)=3x^2+8x\)
La tangente est parallèle à l'axe des abscisses
si et seulement si \(p'(x)=0\)
\(\iff 3x^2+8x=0\)
\(\iff x(3x+8)=0\)
\(\iff x=0 ou 3x+8=0\)
En effet :
\(\color{red}{\text{Un produit de plusieurs facteurs est nul }}\)
\(\color{red}{\text{si et seulement si un des facteurs au moins est nul.}}\)
\(\iff x=0 ou x=\frac{-8}{3}\)
\(p(0)=0^3+4\times 0^2=0\)
\(p(\frac{-8}{3})=(\frac{-8}{3})^3+4\times (\frac{-8}{3})^2\)
\(\iff p(\frac{-8}{3})=\frac{-512}{27}+4\times \frac{64}{9}\)
\(\iff p(\frac{-8}{3})=\frac{-512}{27}+\frac{256}{9}\)
\(\iff p(\frac{-8}{3})=\frac{-512}{27}+\frac{768}{27}\)
\(\iff p(\frac{-8}{3})=\frac{-512}{27}+\frac{768}{27}\)
\(\iff p(\frac{-8}{3})=\frac{256}{27}\)