Exercice : Tangente 3
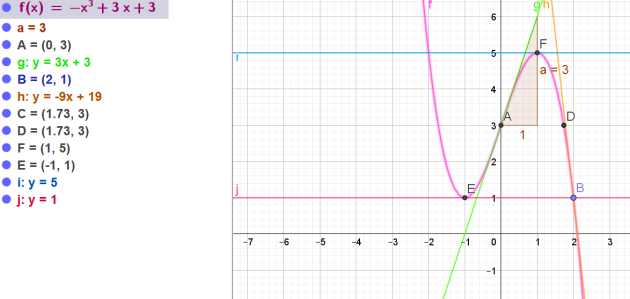
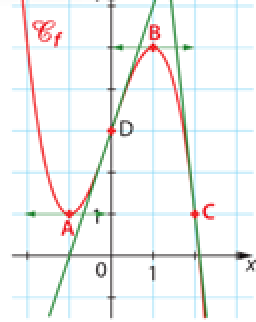
La fonction \(f\) définie sur \(\mathbb{R}\) est connue par sa courbe représentative et quelques tangentes à la courbe en A,B,C et D.
Question
1.Quelle information est donnée par les deux tangentes en A et B ?
Solution
\(f'(-1)=0\)
\(f'(1)=0\)
Question
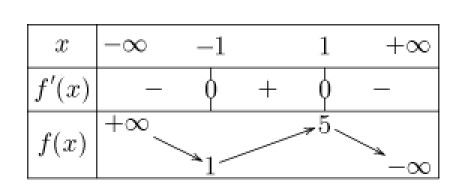
2. Dresser le tableau des variations de la fonction \(f\)
avec le signe de sa dérivée.
Question
3.a.Lire \(f(0)\) et \(f'(0)\)
Solution
\(f(0)=3\)
\(f'(0)=3\)
Question
b.Déterminer l'équation de la tangente à la courbe
\(\mathcal{C}\) au point D.
Solution
Equation de la tangente en \(x=0:\)
\(y=f'(0)(x-0)+f(0)\)
\(\iff y=3(x-0)+3\)
\(\iff y=3x+3\)
Question
c.On donne l'équation réduite de la tangente au point C :\(y=-9x+19.\)
En déduire \(f(2)\) et \(f'(2)\)
Solution
\(f'(2)=-9\)
\(f(2)=-9\times 2+19=-18+19=1\)
Question
4.La fonction \(f\) est une fonction du troisième degré du type :
\(f(x)=ax^3+bx^2+cx+d\)
Déterminer l'expression de la fonction \(f\)
Solution
\(f'(x)=3ax^2+2bx+c\)
\(f'(0)=3a\times0^2+2b\times 0+c=3\)
\(\iff c=3\)
\(f'(-1)=3a\times(-1)^2+2b\times (-1)+c\)
\(\iff 3a\times1-2b+c\)
\(\iff 3a-2b+c=0\)
\(f'(1)=3a\times1^2+2b\times1+c\)
\(\iff 3a+2b+c=0\)
or \(c=3\)
donc \(3a-2b+3=0\)(1)et \(3a+2b+3=0\)(2)
\(6a+6=0 (1+2)\)
\(\iff 6a=-6\)
\(\iff a=-1\)
\(-4b=0(1)-(2)\)
\(\iff b=0\)
donc \(f(x)=-1x^3+3x+d=-x^3+3x+d\)
\(f'(2)=-3\times2^2+3=-9\)
donc la propriété \(f'(2)=-9\) est vérifiée.
\(f(2)=-2^3+3 \times 2+d=1\)
\(\iff -8+6+d=1\)
\(\iff -2+d=1\)
\(\iff d=1+2=3\)
donc \(f(x)=-1x^3+3x+d=-x^3+3x+3\)
\(\color{red}{f(x)=-x^3+3x+3}\)
\(f(0)=-0^3+3\times 0+3=3\)
\(f(1)=-1^3+3\times 1+3=5\)